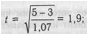А если не получен уровень значимости 0,95? Тогда нужно признать, что нуль-гипотезу не следует отвергать. Впрочем, иногда, по задачам исследования признается достаточным и более низкий уровень. В некоторых исследованиях цель состоит в том, чтобы прийти к утверждению нуль-гипотезы.

Обращаясь к таблицам уровней значимости, исследователь обнаруживает во многих из них специальный столбец с указанием степеней свободы, относящихся к полученному параметру или коэффициенту. Уровень значимости прямо зависит от того, каким числом степеней свободы обладает данный коэффициент или параметр. Число независимых величин, участвующих в образовании того или другого параметра, называется числом степеней свободы этого параметра. Оно равно общему числу величин, по которым вычисляется параметр, минус число условий, связывающих эти величины (Урбах В.Ю. Указ. соч. С. 161). Число степеней свободы и способы его определения всегда даются в окончательных формулах, которыми пользуется исследователь при статистической обработке своих материалов.

Рассмотрим пример с двумя выборками, которые, по мнению исследователя, можно рассматривать как подлежащие обработке параметрическим методом.

Двум группам шестиклассников по 6 человек было дано задание бросать мяч в корзину. Группы обучались по разным программам. Можно ли считать, что разница в программах сказалась на конечной результативности школьников? Для сравнения было взято число попаданий в корзину. Всего было дано по 10 проб.

Формула вычисления Р.

fd (число степеней свободы) = ni + ri2 -2-6 + 6 2-10.

По таблице уровней значимости t Стьюдента находим t0,95= 2,223.

Существенность различия не доказана, хотя полученное значение t = 1,9 очень близко к требуемому уровню. Принимается Н0. Нельзя утверждать, что выборки существенно различаются.

Для вычисления t существует несколько формул, различающихся только техникой расчетов.

Сравниваемые выборки могут быть неодинаковыми по объему. Применять параметрические методы можно лишь к материалу, обладающему определенными свойствами, о которых говорилось ранее. В других случаях следует обращаться к непараметрическим методам.