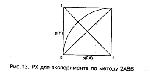
где разность всегда берется от "первой" интенсивности ко "второй", Х1-Х2. Соотношение (27) означает, что функции распределения f(Δx/<S,N>) и f(Δx/<N,S>) являются зеркально симметричными. В этом существенное отличие теоретической схемы для 2АВВ от теоретической схемы для метода "Да-Нет": f(X/S) и f(X/N) могут быть сколь угодно непохожими друг на друга, но f(Δx/<S,N>) и f(Δx/<N,S>) являются зеркальными копиями. Введем в теоретическое представление критерий С*. На рис. 12 заштрихованные области равны по площади вероятностям p(CR) и р(Н). Легко видеть, что несмещенный 2АВВ, при котором p(CR) = р(Н), будет иметь место только в случае С* = 0. При отрицательных С* испытуемый будет более часто правильно указывать сигнал, если сигнальное предъявление было "первым", чем если оно было "вторым" (при этом говорят, что наблюдатель имеет предрасположение к "первому" стимулу). При С*>0 испытуемый имеет предрасположение ко "второму" стимулу: p(CR) > р(Н). Двигая С* справа налево и фиксируя различные пары р(Н), p(FA) (p(FA) = 1 - p(CR)), мы можем построить кривую РХ для 2АВВ (рис. 13).

В силу зеркальной симметричности распределений кривая РХ для 2АВВ всегда симметрична относительно побочной диагонали. Это следствие в принципе позволяет экспериментально проверить валидность схемы с оценкой разностей X1 - Х2, но, к сожалению, строгое статистическое доказательство симметричности РХ провести довольно сложно. В эксперименте различные точки РХ можно получить, задавая асимметричные платежные матрицы (например, штрафуя за пропуск "первого" сигнала значительно больше, чем за пропуск "второго"), подавая одну комбинацию (например, <S,N>) чаще, чем другую и т.д. — совершенно аналогично методу "Да-Нет".

До сих пор мы не использовали предположения о возможности монотонной трансформации Х в Z, при которой f(X/S) и f(X/N) переходят в нормальные распределения f(Z/N) и f(Z/S). 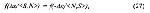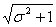Если теперь это предположение принять и использовать разности Zl - Z2, то можно показать следующее: если f(Z/N) имеет центр равным 0 и дисперисию равной 1, a f(Z/S) - центр в точке а и дисперсию равной σ, то f(ΔZ/<S,N>) и f(ΔZ/<N,S>) являются тоже нормальными распределениями с одной и той же дисперсией, равной и с центрами, соответственно, в точках а и -а (см. рис. 14).