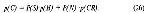P(S) = P(<S,N>), P(N) = P(<N,S>) == 1 - P(S).

Правильный ответ 1 можно условно считать попаданием и обозначать его условную вероятность через р(Н) = р("Да","Нет"/<S,N>); ошибку 2 можно условно считать ложной тревогой и использовать обозначение p(FA) = p("Да","Нет"/<N,S>) и т.д. Аналогично методу "Да-Нет" вводятся платежные матрицы, обратная связь, предварительная информация. Укажем, однако, на одно существенное отличие. Если в методе "Да-Нет" P(S) и платежная матрица таковы, что мы допускаем, что субъективные цены обеих ошибок (FA и О) одинаковы, то вовсе не необходимо, чтобы условные вероятности этих ошибок были равны. Или, что то же самое, нет оснований, вообще говоря, ожидать, что р(Н) = p(CR). В методе 2АВВ, однако, пары <S,N> и <N,S> симметричны и при сделанных предположениях условные вероятности правильных ответов 1 и 2 должны быть равны. Это интуитивное соображение подкрепляется теоретической моделью, к изложению которой мы переходим. Но прежде введем новое обозначение. Условимся через р(С) (от английского correct — правильный) обозначать суммарную вероятность правильного ответа:

Результаты 2АВВ называются несмещенными, если р(Н) = p(CR) или, что то же самое, p(H) + p(FA) = l.

Теоретическая модель 2АВВ является простым распространением модели, изложенной в предыдущем разделе. Мы сразу предположим, что все сделанные там допущения и упрощающие предположения сохраняют свою силу по отношению к <S> и <N> по отдельности, а когда <S> и <М> объединяются в пару, их сенсорные репрезентации независимы друг от друга, причем испытуемый никогда не путает, какому ("первому" или "второму") члену пары соответствует данный образ. Каждый образ оценивается по интенсивности некоторого выбранного качества, так что образ пары оценивается по паре интенсивности сенсорного качества <Х1,Х2>, записанных в той же последовательности, что и стимулы. Если предъявляется <S,N>, то XI имеет распределение f(X/S), X2 — распределение f(X/N). Если предъявляется <N,S>, то наоборот XI распределяется по f(X/N), a X2 — по f(X/S). Имея <Х1,Х2>, испытуемый должен решить, первая или вторая интенсивность соответствует <S>. Естественным правилом решения здесь является следующее: берется разность XI-X2 и сравнивается с критическим значением С*. Если X1 - X2 > С* , то дается ответ "Да, Нет", если же X1 - X2 < С* то "Нет, Да". Как видим, С* играет здесь ту же роль, что и критерий С в методе "Да-Нет". Заметим, что разность берется всегда в одном и том же направлении, скажем от "первой" интенсивности ко "второй", Х1-Х2, независимо от того, было ли предъявлено <S,N> или <N,S>. Начнем с рассмотрения случая предъявления <S,N>. Поскольку X1 и X2 суть случайные величины, то их разность тоже является случайной величиной, распределение которой мы обозначим через f(Δx/<S,N>). f(Δx/<S,N>) есть плотность вероятности того, что X1 - X2 = Δх при предъявлении <S,N>. Эта функция однозначно определяется, если известны два распределения f(X/S) и f(X/N). Пусть теперь предъявлена пара <N,S>. Очевидно, что в этом случае разность X2 – X1 распределена точно так же, как разность X1 - X2 в первом случае, т.е. плотность вероятности события X2 – X1 = Δx/<N,S> равна плотности вероятности события X1 - X2 = Δх/<S,N>; но ведь событие X1 - X2 = Δх/<S,N> равносильно событию X2 – X1 = Δx/<N,S>. Мы получаем важное соотношение: