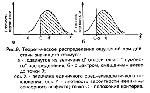
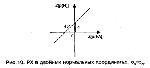
Следовательно:

Допустим теперь, что проведен новый эксперимент с измененными параметрами, так что получена новая пара p(FA) и р(Н). Если наше предположение относительно f (Z/S) и f (Z/N) верно (т.е. они оба нормальны и имеют одну и ту же дисперсию), то, несмотря на изменение величины С прямо определяемой по формуле (14), величина d’, определяемая по формуле (17), должна оставаться постоянной. Мы приходим к важному заключению: если по оси абсцисс откладывать величины Z[p(FA)], а по оси ординат — z[p(H)], то точки РХ должны выстроиться в прямую линию, описываемую уравнением (17): z[p(H)] = z[p(FA)] + d', и наклоненную под 45° к оси абсцисс. График зависимости Z[p(H)] от Z[p(FA)] (см. рис. 10) называется РХ в двойных нормальных координатах. Из соотношения (17) вытекает способ экспериментальной проверки предположений, принятых о нормальности распределений и равенстве дисперсий. Пусть мы провели К экспериментов и получили К точек РХ (К ≥ 2).

Построим РХ в двойных нормальных координатах: z[p(FA)] и z [p(H)j. Поскольку вероятности р(Н) и p(FA) оценивались по частотам (т.е. мы имеем лишь их приблизительные значения), то точки; соответствующие z-преобразованиям, будут отклоняться от теоретической прямой (с наклоном 45 градусов) даже в том случае, если проверяемые предположения верны. Следовательно, надо провести прямую наилучшего приближения и проверить с помощью стандартных статистических средств, значимо или не значимо ее наклон отличается от 45°. Если отличие не значимо, исходные предположения могут считаться верными, а величина свободного члена в формуле прямой дает нам статистическую оценку d'. Разумеется, всем этим выводам должна предшествовать проверка того, является ли расположение экспериментальных точек хорошим приближением к прямой линии, т.е. необходимо провести статистический тест на линейность.

Допустим теперь, что удалось показать, что z-преобразованная РХ не является прямой с наклоном в 45 градусов. Тогда мы можем обратиться к более общему варианту нашей теоретической схемы: допустить, что σs распределения f(z/S) произвольна, но оба распределения нормальны. Очевидно, формула (14) сохраняет свою силу, так как С определяется только по p(FA). Изменения по отношению к случаю с σs,n = 1 появляются лишь в том месте, где распределение f(z/S) вместе с критерием С сдвигается влево до совмещения центра с нулевой точкой. Теперь мы уже не можем написать формулы (15) и (16), так как сдвинутое распределение описывается формулой: . 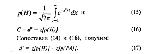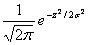Однако, если мы вдобавок к сдвигу сожмем ось Z ровно в σ раз, то распределение приобретет нужную нам табличную форму. При этом критерий С, который после сдвига занял позицию С - а (мы уже не напишем d' вместо а), займет позицию . Итак: