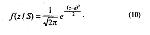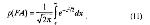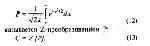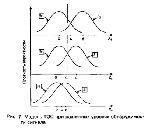
Если допустить, что σs,n = 1, т.е. дисперсии обоих распределений равны, а центр распределения f (Z/S) сдвинут вправо от центра распределения f(Z/N) на величину а, тогда

В этом случае вместо а обыкновенно пишут специальный символ d' и называют эту величину мерой чувствительности наблюдателя к сигналу. Чувствительность к сигналу характеризуется степенью отличия Z-величин, вызываемых <S>, от Z-величин, вызываемых <N>. Чем меньше величина d', тем больше перекрываются области Z-значений, соответствующих <S> и <N> (рис. 7).

Легко видеть, что при одном и том же положении критерия С, а следовательно, при одной и той же величине p(FA), величина р(Н) тем ближе к p(FA), чем меньше d'. Если d' = 0, то p(FA) = р(Н) при всех С и, следовательно, РХ в таком эксперименте совпадает с главной диагональю квадрата (рис. 8). Если d' > 0, РХ лежит выше диагонали и имеет гладкий и симметричный вид относительно побочной диагонали, идущей из (0,1) в (1,0). Чем больше d', тем более выпукла РХ влево-вверх и тем дальше она отстоит от главной диагонали. Как же практически вычислить d' и С по результатам эксперимента? Сколько точек РХ следует для этого иметь?

Оказывается, достаточно только одной точки, т.е. только одной пары p(FA), p(H). Действительно,

Это уравнение необходимо решить относительно С. Введем новый термин: нахождение С по Р в уравнении (12):

Сделать Z-преобразование можно по обычной таблице нормального распределения. Если есть таблица, показывающая для каждого С значение интеграла (12), то нужно попросту отыскать в таблице значение интеграла, наиболее близкое к Р, и посмотреть слева, какому С оно соответствует. Легко показать, что уравнение (11) в терминах Z-преобразования имеет решение:

Теперь допустим, что С найдено. Как, зная р(Н), найти величину d'? Рассмотрим теоретическую картинку, из которой удалено распределение, соответствующее N (оно уже не понадобится, см. рис. 9а). Сдвинем все распределение вдоль оси Z вместе с критерием С влево так, чтобы центр совместился с точкой 0. Критерий С при этом, очевидно, займет позицию (С - d'), а заштрихованная область не изменится и останется равной по площади р(Н) (см. рис. 9б). Но наше сдвинутое распределение имеет центр в нуле и единичную дисперсию.