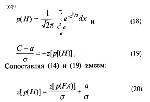Итак, если оба распределения нормальны, то график РХ в двойных нормальных координатах должен быть прямой линией с наклоном 1/σ (см. рис.11). Для проверки предположения о нормальности нужно оценить возможность описания экспериментальных точек линейной функцией или, (другими словами) "хорошесть" подгонки прямой линии к экспериментальным точкам.

На основании статистических оценок предположение о нормальности отвергается, если даже наилучшая (в смысле метода наименьших квадратов, например) прямая плохо подходит к данным.

Предположим, что распределения f(z/S) и f(z/N) имеют одинаковые дисперсии, то есть РХ в двойных нормальных координатах является прямой линией с наклоном 1. Положение каждой отдельной точки на РХ соответствует некоторому положению критерия С.

Можно показать, что при сделанных нами допущениях о нормальности распределений и равенстве дисперсий каждому положению С взаимно однозначно соответствует так называемое отношение правдоподобия (в точке С) — β, которое определяется как:

Здесь f(C/S) и f(C/N) представляют собой значения функций плотности вероятности f(X/S) и f(X/N), взятые в критической точке С. Отношение правдоподобия β характеризует то, во сколько раз правдоподобнее, что сенсорная репрезентация, равная по величине значению С, будет вызвана значащим стимулом, чем стимулом пустым.

По некоторым теоретическим соображениям положение критерия принято характеризовать именно этим значением β, а не самой величиной С.

Значения f(C/S) и f(C/N) легко найти, зная р(Н) и p(FA). Для этого необходимо воспользоваться таблицей плотности нормального распределения: найти значения плотностей, соответствующие Z[p(H)] и Z[p(FA)] (что мы уже умеем делать). Эти значения обозначаются через f[p(H)] и f[p(FA)]. Таким образом:

Оказывается, однако, что не обязательно искать f-преобразования для того, чтобы вычислить β. Вместо этого проще (и полезнее) вычислить lnβ прямо по z-преобразованным вероятностям. Дело в том, что в формулы, выражающие р(Н) и p(FA) через d' и β, последняя входит только в форме lnβ (попытайтесь сами вывести эти соотношения):