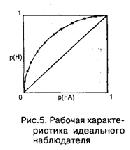
Вернемся теперь к нашей ситуации, где стимул есть либо <S>, либо <N>. Каждому из стимулов соответствует своя функция плотности вероятности: f (X/S) и f (X/N) (рис. 4).

Согласно принятому утверждению, правило принятия решения определяется выбором граничной точки С (ее еще называют критической точкой или величиной критерия принятия решения о наличии сигнала), такой, что если интенсивность Х в данной пробе превышает С, то следует ответ "Да", если же не превышает, то — "Нет". Легко видеть по рисунку, что вероятность ложной тревоги p(FA) равна вероятности того, что интенсивность Х (при условии, что предъявлен <N>) превзойдет С, т.е. равна заштрихованной области под кривой f (X/N). Вероятность попадания р(Н) равна вероятности того, что Х (при условии, что предъявлен <S>) превзойдет С, т.е. равна незаштрихованной области под кривой f (X/S).

Если критерий С находится далеко вправо (показано на рис. 4 одной стрелкой), то, очевидно, p(FA) = p(H) = 0. Если теперь начать двигать критерий справа налево, то при каждом очередном значении мы будем получать новую пару p(FA) и р(Н), причем оба значения будут возрастать (или по крайней мере не убывать), пока при достаточно далеком левом положении С оба не станут равны 1 (показано двумя стрелками на рис. 4). Поскольку каждое значение С однозначно определяет пару чисел p(FA) и р(Н), то ему можно поставить в соответствие точку внутри квадрата (рис. 5), на вертикальной стороне которого откладывается р(Н), а на горизонтальной — p(FA), и таким образом представить результат работы наблюдателя.

Полученная по этим точкам кривая называется рабочей характеристикой наблюдателя или просто — РХ. Любая пара распределений, f (X/S) и f (X/N) однозначно определяет РХ, но обратное неверно: одна и та же РХ может определяться различными парами f (X/S) и f (X/N). РХ идет из точки (0,0) квадрата в точку (1,1) и при этом располагается выше его главной диагонали. Последнее следует из того, что распределение f (X/S) сдвинуто вправо этносительно f (X/N), т.е. р(Н) превышает p(FA). (СНОСКА: Очевидно, что когда наблюдатель фактически не обнаруживает сигнал и p(H) = p(FA), точки РХ будут лежать на диагонали.)