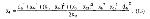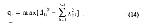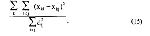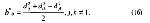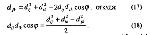Точка, наиболее удаленная от гиперплоскости в пространстве размерности r, ищется из условия:

Процедура продолжается до тех пор, пока сумма всех проекций на k-ю ось не окажется меньше некоторого наперед заданного критерия. Например, эффективность решения можно определять отношением:

Обычно ограничиваются таким количеством осей, которое дает разброс, исчерпывающий до 70-90% дисперсии.

Число полученных осей рассматривается как минимальная размерность субъективного пространства, необходимая, чтобы удовлетворялась совместимость всех межточечных расстояний. Простота этого метода делает его удобным для применения к данным, структура которых имеет линейный характер. Однако получающаяся картина существенно зависит от первоначально взятых расстояний, т.е. решение оказывается зависимым от зашумленности исходных данных. Необходимо также отметить, что результирующее пространство определяется всего по нескольким точкам, и поэтому отдельные изолированные точки могут полностью определить решение задачи (Аустин, Орлочи, 1966). Очевидно, что метод, в котором пространство определяется разбросом всех точек, будет иметь более общий характер. Именно такой метод был предложен Торгерсоном (1952, 1958).

Метод Торгерсона. Метод метрического МШ, описанный в работах Торгерсона (1952, 1958), свободен от большинства недостатков метода ортогональных проекций и дает решение, независимое от начального этапа вычислений. Он основан на процедурах аппроксимации исходной матрицы матрицей меньшего ранга (Янг, Хаусхольдер,1938).

Пусть dij, dik и djk — симметричные расстояния между тремя точками i, j и k. Рассмотрим симметричную матрицу Вi* с элементами b*ij и размерностью (n-1)(n-1), где:

Элемент b*ij представляет собой скалярное произведение векторов от точки i к точкам j и k. Это легко показать с помощью закона косинуса, где для любых трех точек

Из уравнений (16) и (18) следует, что b*ij = dijdikcosφ, т.е. скалярному произведению векторов из точки i к точкам j и k. Любая из n точек может быть взята как точка i. Таким образом существуют n матриц В*, из которых каждая может быть взята как данная матрица скалярных произведений.