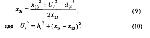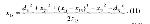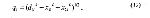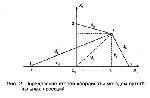
2. Вычисление координат.

К настоящему времени для вычисления координат точек в психологическом пространстве различными авторами разработано большое количество разнообразных алгоритмов. В данной работе рассматриваются только три из них, которые непосредственно использовались для анализа экспериментальных данных.

Метод ортогональных проекций. Одним из наиболее простых метрических методов МШ является метод ортогональных проекций (Орлочи, 1967; Соколов и др., 1975). Суть его заключается в следующем.

Если есть множество точек, заданных расстояниями между ними, то мы можем максимальное из этих расстояний принять за первую ось (Х1). Точки, заданные этим максимальным расстоянием, обозначим как 1 и 2, затем точку 1 на этой оси примем за начало оси Х1 и спроектируем ортогонально все остальные точки на ось Х1. Тогда точка 1 имеет координату Х11 = 0, а точка 2 — координату X12 = d12.

Величина проекции для каждой точки i (кроме первых двух точек) вычисляется по известной геометрической формуле:

Далее легко вычисляются расстояния от каждой точки до оси X1 по формуле:

Если все hi = 0, то очевидно, что все точки лежат на оси X1, т.е. пространство данных точек одномерно. Если некоторые hi > 0, то из них выбирается максимальное (hmax) и принимается за ось Х2, то есть hmax = X23, а точка пересечения hmax с осью X1 есть начало оси X2 (рис.2).

Затем все остальные точки ортогонально проецируются на ось Х2 и величина проекции вычисляется по формулам:

Объединив эти формулы, получим:

Расстояние от каждой точки до плоскости Х1Х2 определится теперь как

И в этом случае, если все qi = 0, то, следовательно, все точки лежат на плоскости Х1Х2 и выделение следующей оси пространства не имеет смысла.

Далее, если qi отличны он нуля, то выбирается точка с максимальным значением — qmax и принимается за четвертую точку, и тогда через эту точку 4 будет проходить ось Х3. Далее вычисляются проекции всех остальных точек на эту ось: