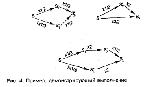
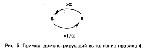
4. Если Z1 = Z2 ∙ α, то Z2 = Z1 ∙ 1/α (это свойство обратимости). (СНОСКА: Это правило формально выводимо из правила 2, но для удобства его выделяют отдельно.)

Рассмотрим, что означают эти правила на языке эмпирических операций деления (умножения):

1. Свойство 1 выполняется очевидно всегда, если только нет систематических ошибок, связанных с условиями эксперимента.

2. Пусть испытуемый "делит" стимул S на 2, тем самым он выбирает новый стимул S’1. Стимул S’1 он "делит" на 3 — выбирает стимул S'2. Если бы первое "деление" было не на 2, а на 3, то вместо S'1 должен был бы выбираться некоторый стимул S''1. Правило 2 гарантирует, что если теперь S"1 "разделить" на 2, то получится опять S'2 (т.к. 1/3 ∙ 1/2 = 1/2 ∙ 1/3). Этот пример, а также и другие примеры, демонстрирующие проверку правила 2, приведены на рис. 4.

3. Правило 3 означает, что путем каких-то "умножений" и "делений" от одного стимула всегда можно "добраться" до любого другого. Если эксперимент организован так, что это правило выполняется, то мы избавляемся от необходимости строить психофизическую зависимость приблизительно (ведь до любого стимула можно "добраться" от "единичного" и тем самым получить точно соответствующее ему шкальное значение).

Можно доказать следующее утверждение: если экспериментально построены не одна кривая "деления на n" (см. рис. 1), а две — "деления на m" и "деления на n", где n и m — взаимно простые числа (например, 2 и 3), то правило 3 выполняется. Доказательство следует из того факта, что любое шкальное значение может быть сколько угодно точно приближено числом вида 2a ∙ 3b (а, b = 0, ±1, ±2,...).

4. Правило 4 поясняется на рис. 5.

Здесь, как и на рис. 4, стрелка обозначает выбор нового стимула. Проверка выполнимости правила может быть осуществлена так: строится кривая "деления на n" и кривая "умножения на n", они должны совпасть с точностью до перемены осей (как функции ln и ехр).