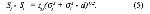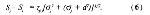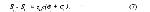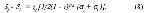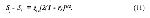Но практически выражения (4) и (5) идентичны, поскольку ковариация является постоянной только тогда, когда корреляция стремится к нулю.

IV вариант Терстоуна основывается на допущении, что ri,j = 0 и что дисперсии различения мало отличаются друг от друга, т.е. si = sj + d, где d мало по сравнению с sj. Тогда выражение (3) преобразуется в

Раскрывая скобки и делая ряд преобразований и упрощений, получаем окончательную форму четвертого варианта закона:

где с — постоянный множитель.

Более слабое допущение Торгерсона (условие В) о константности корреляции приводит к выражению:

Выражения (7) и (8) отличаются только постоянными членами, поэтому вариант Торгерсона имеет определенные преимущества.

V вариант закона сравнительных оценок Терстоуна нашел наибольшее применение вследствие простоты своей формы. Этот вариант основывается на допущении нулевой корреляции между двумя процессами различения (r = 0) и равенства различительных дисперсий этих процессов (σj = σi = σ). Тогда выражение (4) преобразуется в:

Обозначив константный член уравнения буквой "с", получим:

Уравнение (10) совпадает по своей общей форме с различными модификациями данного варианта, которые предлагали впоследствии некоторые авторы. Наиболее интересная модификация предложена Мостеллером (1951) и состоит в допущении равенства дисперсий и константной корреляции. В этом случае величина "с" в уравнении (10) будет равна [2(1 - r)]1/2, а уравнение приобретает следующий вид:

Сравнивая упрощенные варианты (4), (7), (10) с исходной формулой (3), легко видеть, что даже наиболее сложный из упрощенных вариантов (4) уже имеет, по крайней мере теоретически, решение, когда число стимулов (n) равно 5. Остальные варианты еще проще. Но практическая процедура всегда более трудоемка и менее изящна, чем это обещает теоретическая модель. Причина этого в основном лежит в эмпирической природе исходных оценок, в их зашумленности множеством случайных факторов, от которых невозможно оградить испытуемого. Для устранения случайных ошибок предлагается следующая тактика. Число стимулов увеличить так, чтобы система уравнений была значительно переопределена. Например, для варианта III брать не 5 стимулов, а 10 — 15. Для окончательного решения использовать итеративную вычислительную процедуру, которая учитывает тот факт, что случайные ошибки имеют тенденцию взаимоуравновешиваться.