| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Гусев А. Н., Измайлов Ч.А., Михалевская М.Б. Измерение в психологии: общий психологический практикум. / 2-е изд. -- М.: Смысл, 1998. - 286 с. - (Серия «Практикум». Вып. 2).
Стр. 111 Такие процедуры были разработаны разными авторами, и в данной работе будет описан алгоритм Мостеллера (1951) для V варианта закона в модификации Торгерсона (1958). Алгоритм использует решение методом наименьших квадратов. Он позволяет получить более точные оценки шкальных значений из матрицы в случае, если она не имеет пустых элементов. §4. Процедура решения V варианта закона сравнительных оценок для полной матрицыВ V варианте закона, записанном в общем виде (9), единицы измерения шкальных значений всегда можно подобрать так, чтобы константа "с" была равна 1. Тогда: В случае отсутствия ошибок в оценках искомое различие будет равно наблюдаемому (обозначим его z'j,i). Но в результате ошибок между z'j,i и z.j,i будет некоторое расхождение σ. Задача заключается в получении такого множества оценок шкальных значений стимулов, для которых сумма квадратов всех расхождений является минимальной, т.е. необходимо минимизировать величину Подставив вместо zi,j идеальные значения, получим: Все аi,j для всех zi,j из матрицы Z дадут матрицу ошибок α.. Чтобы минимизировать каждую αi,j, необходимо взять частную производную αi,j по Si и Sj. Каждое частное значение Si в матрице ошибок а появляется только в i-той строке и i-том столбце, но поскольку матрица ошибок так же кососимметрична [zi,j = -zj,i и (Si - Sj) = - (Sj - Si)], как и матрица Z, то для каждой Si частная производная будет касаться только i-гo столбца. Дифференцируя элементы каждого столбца по Si, получим: Приравняем частную производную нулю и после переноса получим: Разделим выражение (16) на n и возьмем начальное значение шкалы, равное Таким образом, для минимизации ошибки необходимо просто взятъ среднее арифметическое по столбцу матрицы Z и мы получим оптимальное значение шкальной величины Si. Рассмотрим практический пример решения V варианта закона сравнительных оценок методом наименьших квадратов (данные вымышлены). Испытуемому в случайном порядке предъявляются 6 цветных карт из малого набора теста Люшера и просят в каждой паре выбрать наиболее красивый. Каждая пара предъявляется по 50 раз. В итоге для одного из испытуемых была получена следующая матрица частот F (табл.1): |
Реклама
|
||

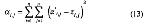
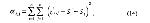
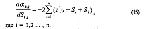
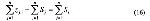
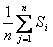 . В результате получим:
. В результате получим: