| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Компетентность и проблемы ее формирования в системе непрерывного образования (школа – вуз – послевузовское образование) / науч. ред. проф. И.А. Зимняя; Материалы ΧVΙ научно-методической конференции «Актуальные проблемы качества образования и пути их решения». –– М.: Исследовательский центр проблем качества подготовки специалистов, 2006. – 130 с.
Стр. 134 Предположим, что в базе знаний по каждому разделу имеется некоторое множество различных комбинаций понятий. Это говорит о существовании набора подмножеств Хп,...,Xis< множества Xi. Данные множества могут быть сформированы различными способами, основываясь на каких-либо принципах. Рассмотрим для определенности ситуацию, когда на сформированных подмножествах задано отношение частичного порядка, то есть Xi1 Обучающиеся изначально обладают разным уровнем знаний по изучаемой дисциплине. Уровень начальных знаний можно определить путем тестирования и выставления оценок, например, по трехзначной шкале от 3 до 5. Оценка «3» по какому-либо разделу будет свидетельствовать о довольно слабом представлении изучаемого материала, и потребуется глубокое ознакомление с ним. Оценка «5» говорит о возможности изучения только понятий самых высоких уровней. Возможно выделение пятизначных и других шкал, в зависимости от уровня подготовленности обучающегося. В связи с вышесказанным далее предлагается разбить множества доступных вариантов преподавания каждого раздела на три группы, соответствующие оценкам, которые студент может получить при тестировании. Таким образом, с помощью предварительного определения начальных знаний об изучаемом предмете сужается круг допустимых вариантов по каждому разделу. Без ограничения общности далее можно считать, что пространство допустимых вариантов после перенумерации представляет собой декартово произведение множеств |
Реклама
|
||
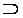 Xi
Xi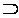 …
…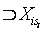 . При этом будем далее считать, что каждое множество Xij составлено путем удаления из Xij-1 некоторых
. При этом будем далее считать, что каждое множество Xij составлено путем удаления из Xij-1 некоторых  понятий, которые студент может опустить при изучении в случае их знания. Таким образом, в Хi1 будет содержаться максимально возможное количество информации, доступной по i-му разделу, в то время как при изучении множества понятий Xis
понятий, которые студент может опустить при изучении в случае их знания. Таким образом, в Хi1 будет содержаться максимально возможное количество информации, доступной по i-му разделу, в то время как при изучении множества понятий Xis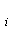 . будут затронуты только знания самых высоких уровней.
. будут затронуты только знания самых высоких уровней.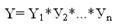 , где
, где 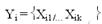 множество доступных вариантов по i-му разделу. Мощность пространства решений равна
множество доступных вариантов по i-му разделу. Мощность пространства решений равна 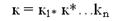 . Предположим также, что для каждого варианта Xij задан показатель ожидаемого эффекта
. Предположим также, что для каждого варианта Xij задан показатель ожидаемого эффекта 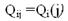 и показатель затрат (например, временных)
и показатель затрат (например, временных) 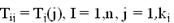 . Зависимости Qi,(j) и Tt{j) являются некоторыми монотонно невозрастающими функциями. Требуется выбрать по одному варианту обучения каждого раздела, чтобы суммарный ожидаемый эффект от изучения курса был максимален, а затраты минимальны. В данном случае наиболее естественным является введение в рассмотрение, например, функционала
. Зависимости Qi,(j) и Tt{j) являются некоторыми монотонно невозрастающими функциями. Требуется выбрать по одному варианту обучения каждого раздела, чтобы суммарный ожидаемый эффект от изучения курса был максимален, а затраты минимальны. В данном случае наиболее естественным является введение в рассмотрение, например, функционала