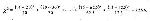| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Татарова Г.Г. Методология анализа данных в социологии (введение) /Учебник для вузов. —— М.: NOTA BENE, 1999. — 224 с.
Стр. 167 Упомянутый выше «язык» анализа локальных связей ¾ язык детерминации ¾ достаточно легко переводится и на многомерный случай. Однако к работе [13] следует обращаться, имея определенный уровень математической подготовки. Меры связи, основанные на c2 (хи-квадрат) Представим себе, как будет выглядеть наша таблица сопряженности в ситуации статистической независимости между феноменами «будущая профессия» и «удовлетворенность учебой». Нетрудно вспомнить, что при статистической независимости, например, для частоты в ячейке (1,4) выполняется соотношение: Если теперь записать это в общем виде, т. е. для любой ячейки (i j), то в случае статистической независимости будет верно соотношение:
Эту частоту, для ее отличия от реальной, можно назвать теоретической и обозначить через Таблица 3.4.4. Таблица сопряженности: реальные и теоретические частоты Является естественным для определения отклонения от статистической независимости воспользоваться разностью между реальными частотами и теоретическими (для случая статистической независимости), т.е. разностью вида
Для нашего примера эта величина вычисляется как сумма тридцати членов: Эта величина, эта статистика знаменита тем, что имеет закон распределения, который называется законом распределения хи-квадрат. Поэтому с ее помощью решается много различных задач, проверяются различные статистические гипотезы. Нас пока интересует только аспект использования величины хи-квадрат для конструирования мер связи. Самой этой величиной как мерой связи неудобно пользоваться, ибо ее значение может быть каким угодно большим и зависит от размера таблицы сопряженности. Различие в коэффициентах, основанных на хи-квадрат, заключается в определенном нормировании величины хи-квадрат. Одним из часто используемых коэффициентов является коэффициент взаимной сопряженности Пирсона. Он имеет следующий вид: |
Реклама
|
||
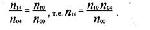
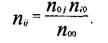
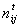 . В таблице 3.4.4 приведены наши реальные частоты, взятые из таблицы 3.3.1, и теоретические. Первые из них — в верхнем левом углу ячейки, а вторые — в нижнем правом углу ячейки.
. В таблице 3.4.4 приведены наши реальные частоты, взятые из таблицы 3.3.1, и теоретические. Первые из них — в верхнем левом углу ячейки, а вторые — в нижнем правом углу ячейки.
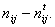 Как и в случае введения формулы для вычисления дисперсии, нам нужны абсолютные значения этой разности, поэтому возводим ее в квадрат. Этот квадрат делим на теоретическую частоту, т. е. как бы нормируем. Тем самым достигается независимость от объема ячейки. Все ячейки становятся равноправными независимо от их объема. Затем суммируем все эти отклонения по всем 30-ти ячейкам таблицы и получаем величину называемую хи-квадрат. Она выглядит следующим образом:
Как и в случае введения формулы для вычисления дисперсии, нам нужны абсолютные значения этой разности, поэтому возводим ее в квадрат. Этот квадрат делим на теоретическую частоту, т. е. как бы нормируем. Тем самым достигается независимость от объема ячейки. Все ячейки становятся равноправными независимо от их объема. Затем суммируем все эти отклонения по всем 30-ти ячейкам таблицы и получаем величину называемую хи-квадрат. Она выглядит следующим образом: