| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Татарова Г.Г. Методология анализа данных в социологии (введение) /Учебник для вузов. —— М.: NOTA BENE, 1999. — 224 с.
Стр. 141
Этим соотношением и воспользуемся для введения коэффициента качественной вариации. Вначале предположим, что номинальный признак имеет только две градации, причем в первую градацию попало N1 объектов, а во вторую ¾N2 объектов {число всех объектов равно n = N1 + N2,). И если теперь в соотношение между средней арифметической и средней геометрической подставить Максимальное значение N, N2 будет только в случае N1 = N2 , и оно будет равно п2 / 4. А это ведь случай равномерного распределения. Коэффициентом качественной вариации и будет отношение реального значения произведения ( N • N2) к максимальному его значению, равному n2 / 4 . Коэффициент равен нулю, если все объекты в одной градации, и единице, если распределение равномерное. Коэффициент легко обобщается на случай, когда число градаций равно k. Представим себе, что из всей совокупности объектов мы образовали всевозможные пары. Вспомним метод парных сравнений Терстоуна и вычисление числа всевозможных пар для сравнения объектов. Здесь ситуация аналогичная. Пары не повторяются, объект сам с собой пару не образует. В случае двух градаций произведение (N1 N2) есть не что иное, как число пар, различных между собой. Если градаций три и по ним частоты равны (N1, N2, N3), то число различных пар будет равно
Число членов в этой сумме вычисляется как число парных сочетаний из трех элементов по два. Вспоминаем, что это число равно k(k-l)/2, когда число элементов равно k. Тогда коэффициент вариации вычисляется как отношение: § реального числа различных пар, равного (N1×N2 + N1×N3 + N2×N3); § к максимальному (случай равномерного распределения), равному В общем случае для k градаций реальное число пар равно Таким образом, формула для вычисления коэффициента качественной вариации приведена по частям, т. е. отдельно числитель (реальное) и отдельно знаменатель (максимальное). |
Реклама
|
||
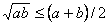
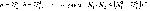
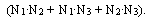
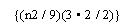 . В первых круглых скобках ¾ то, во что превращается каждый член суммы, а во вторых ¾ число членов в этой сумме.
. В первых круглых скобках ¾ то, во что превращается каждый член суммы, а во вторых ¾ число членов в этой сумме.