| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Татарова Г.Г. Методология анализа данных в социологии (введение) /Учебник для вузов. —— М.: NOTA BENE, 1999. — 224 с.
Стр. 140 Почему имеет смысл средняя арифметическая для дихотомической шкалы? Потому что она содержательно интерпретируется. Если Таким образом, как это ни парадоксально, можно вычислять среднее арифметическое по признаку «пол». Только важно правильно интерпретировать полученный результат, исходя из того, каким образом закодирован этот признак. Разумеется, социологу нет никакого смысла в использовании такого рода средней, отражающей «центральную тенденцию». Он прекрасно работает с относительными частотами в %. Приведенная средняя интересна не для целей первичного анализа, а для анализа с применением сложных математических методов. К примеру, для такой средней можно подсчитать дисперсию. Если для дихотомических признаков имеет смысл использование характеристик метрической шкалы, значит, возможно использование и математических методов, работающих с метрическими данными. Дисперсия в данном случае равна: Эта дисперсия и является мерой вариации для бинарного (дихотомического) признака. При этом она равна нулю, если все объекты либо обладают, либо не обладают анализируемым свойством. Что естественно, так как в этих случаях разброса в данных не наблюдается. Максимальное значение этой дисперсии достигается в случае равномерного распределения (k = n/2), и оно равно 1/4. При этом Напомню вам одно правило из школьной арифметики. Если есть два целых числа, то среднее геометрическое этих чисел всегда меньше или равно среднему арифметическому. Равенство достигается, когда числа равны. |
Реклама
|
||
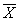 = 0, то это означает, что все студенты-гуманитарии в нашей выборке не социологи. Если
= 0, то это означает, что все студенты-гуманитарии в нашей выборке не социологи. Если