| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Татарова Г.Г. Методология анализа данных в социологии (введение) /Учебник для вузов. —— М.: NOTA BENE, 1999. — 224 с.
Стр. 139 Другие меры вариации Рассмотрим меру вариации, меру отклонения, меру рассеяния значений признака вокруг медианы. Такой мерой является квартильный размах, с которым мы встречались при построении шкалы Л. Терстоуна. Вспомним, что содержательно это интервал, в котором вокруг медианы сосредоточилось 50% экспертов. Это единственная мера вариации для порядковых шкал. На рис. 3.2.4 три пунктирные линии проведены для определения медианы и соответствующего ей квартильного размаха {он равен Перейдем к самым трудным для понимания мерам ¾ мерам качественной вариации, т. е. мерам вариации для признаков, измеренных по номинальным шкалам. Самое главное, что любая такая мера характеризует степень отклонения распределения признака от равномерного, т. е. когда каждой градации признака соответствует одно и то же число объектов. Максимальное значение меры обычно соответствует ситуации равномерного распределения, а минимальное ¾ ситуации, когда все объекты сосредоточены в одной градации. Как мы знаем, любой номинальный признак сводится к совокупности бинарных, дихотомических, т. е. принимающих значения 0 или 1. В этом случае столбец нашей исходной матрицы данных «объект-признак», соответствующий одному признаку, превращается как бы в несколько столбцов, каждый из которых соответствует отдельному свойству (быть социологом, быть политологом и т. д.). Анализировать мы должны теперь поведение «свойства», а не признака. По всем объектам это совокупность из нулей и единиц.
Предположим, что этот ряд получен по свойству ¾ быть в будущем социологом. Если i-й студент ¾ социолог, то ему соответствует хi =1 , а если он не социолог, то хi = 0. Оказывается, для такого вида данных имеет смысл среднее арифметическое. Она равна |
Реклама
|
||
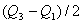 }. Без сравнительного контекста трудно сказать, мало это или много. Для социолога познавательная возможность любого математического конструкта, а это пока простейшие формулы на уровне обыденного понимания, определяются только в сравнительном контексте, т. е. при сравнении значений, полученных в разных условиях.
}. Без сравнительного контекста трудно сказать, мало это или много. Для социолога познавательная возможность любого математического конструкта, а это пока простейшие формулы на уровне обыденного понимания, определяются только в сравнительном контексте, т. е. при сравнении значений, полученных в разных условиях.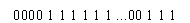
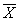 = k/n, где k ¾ число будущих социологов, a n ¾ число всех студентов-гуманитариев.
= k/n, где k ¾ число будущих социологов, a n ¾ число всех студентов-гуманитариев.