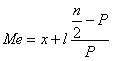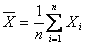В случае нашего примера метрической шкалы ¾ продолжительность затрат времени на учебу ¾ медиана может быть вычислена таким же образом. Для этого проведем упорядочение студентов по возрастанию/убыванию этих затрат и найдем середину аналогичным образом. Медиану можно вычислить и по кумуляте (см. шкалу Терстроуна).

Для порядковых и метрических шкал необходимым является понятие медианного интервала, т.е. интервала содержащего медиану. Как правило, вы не любите формулы, поэтому приведем вербальное описание формулы для вычисления медианы в медианном интервале. Это делается по двум соображениям. Первое ¾ показать, что математическая формула всегда отражает содержание. Второе ¾ математической формулой иногда пользоваться удобнее для избежания очень длинных описаний. Итак, медиана в медианном интервале вычисляется по формуле:

Эту формулу можно записать очень просто с использованием обозначений, приведенных внизу:

Чем выше уровень измерения, тем богаче возможности описания «поведения» признака. Если признак измерен по метрической шкале, то кроме моды и медианы для описания поведения признака используется известная всем мера центральной тенденции ¾ средняя арифметическая.

Среднее арифметическое

Для любой совокупности значений признака это сумма всех значений, деленная на их число. Вернемся к примеру признака ¾ продолжительность затрат времени на учебу. Обозначим число студентов-гуманитариев через n (для нашего случая n=1000), а через Xi: — значение этой продолжительности для i-го студента. Тогда средняя арифметическая продолжительности будет равна:

Таким образом можно определить среднею продолжительность затрат времени на учебу в группах студентов с любой «будущей профессией», с любой степенью удовлетворенности учебой и т. д.

Социолог часто встречается с ситуацией, когда конкретные значения признака по отдельным объектам неизвестны. Исходно имеются только интервалы изменения признака и частота (абсолютная или относительная) встречаемости объектов в этих интервалах. Например, та же продолжительность может быть задана в виде интервалов и частоты в них. Это может быть в двух случаях. Первый ¾ данные о продолжительности получены c помощью прямого вопроса анкеты: «Сколько времени Вы в среднем в неделю тратите на занятия, связанные с учебой?». При этом предлагаются заданные заранее интервалы. По сути, мы имеем дело с порядковой шкалой. В этом случае также можно вычислить среднее значение продолжительности для некоторой группы студентов. Только она называется средняя взвешенная и вычисляется несколько по-другому.