| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Татарова Г.Г. Методология анализа данных в социологии (введение) /Учебник для вузов. —— М.: NOTA BENE, 1999. — 224 с.
Стр. 135 Второй случай, когда у социолога отсутствуют конкретные значения по каждому объекту в ситуации вторичного анализа. Вторичным анализом социолог называет анализ «чужих» данных для решения своих собственных, новых задач. Тогда часто приходится работать уже с вычисленными до него средними арифметическими. Например, результаты исследования бюджетов времени обычно публикуются в виде средних затрат времени с указанием объема группы, для которой они получены. В процессе вторичного анализа возникает необходимость объединения каких-то групп и, соответственно, в подсчете общей средней. В этой ситуации также необходима средняя взвешенная для вычисления «средней средних». Вычислим среднюю продолжительность затрат времени на учебу студентами-гуманитариями по данным таблицы 3.1.3. Для этого предполагается, что продолжительность для каждого респондента, отнесенного к интервалу, равна середине интервала. Для наших шести интервалов их середины соответственно равны: Х1 = 0,5; X2 = 1,75; X3 = 3,25; X4 = 5,5; X5 = 7,5; X6 = 8,5. Нам известно число студентов в каждом интервале: n1 = 27; n2 = 75; n3 = 150; n4 = 348; n5 = 250; n6 = 150. Тогда продолжительность затрат времени на учебу в среднем на студента или средняя взвешенная продолжительность равна: Формула для вычисления средней взвешенной выглядит для k интервалов следующим образом:
где Xj ¾ середина j-го интервала. Аналогично вычисляется «средняя средних». Допустим, перед социологом стоит задача вычисления средней продолжительности жизни мужчин в России по данным отдельных областей. Эти данные представляют собой среднюю продолжительность жизни мужчин по каждой области. Естественно, «среднюю средних» вычисляем с весами, равными численности мужчин в каждой области. Все рассмотренные характеристики: мода, медиана, средняя арифметическая, среднее взвешенное ¾ являются средними. Они характеризуют центральные тенденции одномерного распределения. Есть и другие средние, но они в социологии применяются редко. Поэтому среднюю арифметическую называют просто средней, а мода и медиана сохраняют свои названия. Без процедуры усреднения социолог-эмпирик существовать не может. Другое дело, с помощью каких средних он проводит эту процедуру. |
Реклама
|
||
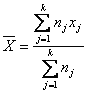 ,
,