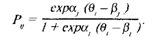| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Дружинин В.Н. Экспериментальная психология: Учебное пособие — М.: ИНФРА-М, 1997. -- 256 с.
Стр. 218
где θ — среднее значение логитов уровней способностей, V — стандарное отклонение распределения начальных значений "способности", n — число заданий в тесте. Эти эмпирические оценки используются в качестве окончательных характеристик измеряемого свойства и самого измерительного инструмента (заданий теста). Если перед исследователем стоит задача конструирования теста, то он приступает к получению характеристических кривых заданий теста. Характеристические кривые могут накладываться одна на другую. В этом случае избыточные задания выбраковываются. На определенных участках оси 9 ("способность") характеристические кривые заданий могут вовсе отсутствовать. Тогда разработчик теста должен добавить задания недостающей трудности, чтобы равномерно заполнить ими весь интервал шкалы логитов от — 6 до +6. Заданий средней трудности должно быть больше, чем на "краях" распределения, чтобы тест обладал необходимой дифференцирующей (различающей) силой. Вся процедура эмпирической проверки теста повторяется несколько раз, пока разработчик не останется доволен результатом работы. Естественно, чем больше заданий, различающихся по уровню трудности, предложил разработчик для первичного варианта теста, тем меньше итераций он будет проводить. Главным недостатком модели Раша теоретики считают пренебрежение "крутизной" характеристических кривых: "крутизна" их полагается одинаковой. Задания с более "крутыми" характеристическими кривыми позволяют лучше "различать" испытуемых (особенно в среднем диапазоне шкалы способности), чем задания с более "пологими" кривыми. Параметр, определяющий "крутизну" характеристических кривых заданий, называют дифференцирующей силой задания. Он используется в двухпараметрической модели Бирнбаума. Модель Бирнбаума аналитически описывается формулой
Параметра определяет "крутизну" кривой в точке ее перегиба. |
Реклама
|
||
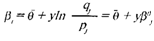 , где
, где