| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Дружинин В.Н. Экспериментальная психология: Учебное пособие — М.: ИНФРА-М, 1997. -- 256 с.
Стр. 215 В классической теории теста индивидуальный балл (уровень свойства) считается некоторым постоянным значением. В IRT латентный параметр трактуется как непрерывная переменная. Первично моделью в IRT стала модель латентной дистанции, предложенная Г.Рашем: разность уровня способности и трудности Tecia х — р , где х — положение i-ro испытуемого на шкале, ар — положение j-ro задания на той же шкале. Расстояние (х — р ) характеризует отставание способности испытуемого от уровня сложности задания. Если разница велика и отрицательна, то задание не может быть выполнено, так как для данного испытуемого оно слишком сложно. Если же разница велика и положительна, то задание также не информативно, ибо испытуемый заведомо легко и правильно его решит. Вероятность правильного решения задания (или ответа "да") i-м испытуемым:
Вероятность выполнения j-ro задания группой испытуемых:
В IRT функции (х) и f(P) называются функциями выбора пункта. Соответственно первая является характеристической функцией испытуемого, а вторая — характеристической функцией задания.
Считается, что латентные переменные х и (3 нормально распределены, поэтому для характеристических функций выбирают либо логистическую функцию, либо интегральную функцию нормированного нормального распределения (как мы уже отмечено выше, от, мало отличаются друг от друга). Поскольку логистическую функцию проще аналитически задавать, ее используют чаще, чем функцию нормальною распределения. Кроме "свойства" и "силы пункта" (она же — трудность задания 1 в аналитическую модель IRT могут включаться и другие переменные. Все варианты IRT классифицируются по числу используемых i, них переменных. Наиболее известны однопараметрическая модель Г.Раша. двухпараметрическая модель А.Бирнбаума и трехпараметрическая модель А.Бирнбаума. В однопараметрической модели Pauia предполагается, чтоотвеч испытуемого обусловлен только индивидуальной величиной измеряемого свойства (й ) и "силой" тестового задания ([3). Следовательно, для верного ответа ("да") и для неверного ответа ("нет") |
Реклама
|
||
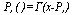
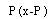 .
.