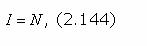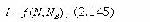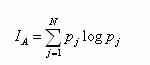Абсолютное количество информации определяется только числом различимых информационных элементов N, т.е.

Относительное количество информации характеризует рассматриваемую систему взаимных связей между N и каким-то базисом Nв, относительно которого определяется количество информации. В качестве такого базиса может служить базисное число различимых элементов информации (семантических единиц) или какой-то показатель качества функционирования, например, вес "ущерба", степень достижения цели.

В общем случае при определении относительного количества информации имеет место приведение:

где: f - функция, количественно отображающая оценку взаимных связей N элементов информации относительно принятого базиса NB.

Так, если функция f имеет вид логарифмической функции, NB=1, а при измерении различимых единиц информации N в сообщении их взаимные связи не учитываются, т.е. I=logN, то получим известное выражение Хартли. Если f представить сложной функцией вида (2.93), в качестве базиса рассматривать NB=1 эсед и учитывать взаимосвязь в сообщении отдельных семантических (смысловых) элементов информации N, то получим оценку смысловой емкости сообщения или оценку количества семантической информации в смысловой структуре.

Выражение (2.145) в общем виде характеризует относительное количество информации, в том числе и семантической (смысловой), когда аргументами N, NB являются различимые элементы информации, например, семантические единицы, и при этом различимость этих элементов рассматривается только с точки зрения количественных характеристик образованного ими сообщения (смысловой структуры), а между собой при этой оценке они никак не различаются.

Но в (2.145) аргументами могут рассматриваться не только сами информационные элементы (семантические единицы), а сопутствующие им признаки, которые характеризуют их с каких-то позиций. Если в качестве Nj взять априорную вероятность рj появления события А, которое идентифицируется с j-ым элементом информации, а NB принять равным единице и предположить, что r имеет логарифмический вид, то получим формулу Шеннона, характеризующую математическое ожидание относительного количества информации, заключенной в N ее элементах в предположении их аддитивности:

В свою очередь, если в качестве характеризующего Nj элемент информации признака принять какой-то из показателей качества его реализации в отношении определенной цели функционирования системы, а Nвj - нормативное (эталонное) значение этого показателя, то определенное относительное количество информации будет иметь прагматическое содержание, т.е. отображать ценность (полезность) реализации рассматриваемого элемента информации для целей функционирования системы. В соответствии с этим показателем ценности (полезности) информации будет функция чувствительности степени достижения рассматриваемой j-ой цели к i-му количеству информации: