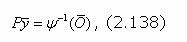| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 369 - для абсолютного большинства задач управления функцию y достаточно представить одной из четырех зависимостей: линейной, степенной, логарифмической и экспоненциальной. Если в (2.127, 2.128) функция f есть функция y приведения рассматриваемой неорганизованности yj к вышестоящему показателю yв, то такая неорганизованность называется "приведенной неорганизованностью". Тогда для приведенной неорганизованности (2.128) примет вид:
где y - функция чувствительности вышестоящего показателя yв к изменению yj
Рассмотрим одно из частных выражений для приведенной неорганизованности, из которого могут быть получены все основные выражения для информации и энтропии. Будем исходить из выражения (2.127) и допустим, что имеется m ситуаций, l=1, d=1, а вероятность появления каждой j-ой ситуации рj. Введем показатель wj - вес каждой ситуации, учитываемый при их объединении. В этом случае можно говорить об ансамбле ситуаций
Полагая, что обобщение в (2.127) осуществляется в предположении аддитивности отдельных ситуативных неорганизованностей, получим Здесь Pyj - параметр неупорядоченности, который соответственно находится для абсолютной, относительной и степенной неупорядоченности из выражений:
wj - веса неупорядоченностей, учитываемые при их объединении. Исходя из (2.130) и указанных выше характеристик функции Y, получим основные выражения для апостериорной оценки единичных приведенных неорганизованностей: где: C, k, a, n - соответственно постоянные коэффициенты и степенная зависимость. Если при той или иной заданной зависимости y из (2.130) найдено значение обобщенно неорганизованности О, то используя обратную функцию Y-1, можно получить соответствующее этой неорганизованности значение обобщенного параметра неупорядоченности:
Отсюда в системно-информационной анализе определяется система правил для сложения (объединения) и вычитания (различия) однотипных неорганизованностей с точностью до постоянных С. Для объединения однотипных и независимых неорганизованностей необходимо сначала получить их отображения на множестве параметра неупорядоченности, сложить (или перемножить) значения этих отображений, а затем полученный результат опять отобразить на множество неорганизованности, т.е. |
Реклама
|
||
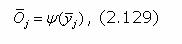
 Если в качестве вышестоящего показателя yв выступает оценка ЛПР, отображающая систему его предпочтений в отношении функционирования системы, то (2.127) есть объективная оценка неорганизованности yj в системе предпочтений ЛПР.
Если в качестве вышестоящего показателя yв выступает оценка ЛПР, отображающая систему его предпочтений в отношении функционирования системы, то (2.127) есть объективная оценка неорганизованности yj в системе предпочтений ЛПР.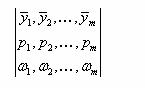
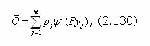
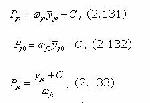
 где: С - коэффициент, определяемый из условия yj =0 при Y(Pj)=0
где: С - коэффициент, определяемый из условия yj =0 при Y(Pj)=0