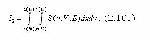1. Восприятие обучаемым условий познавательной задачи (НС и КС) и выбор (определение) образа соответствующей субъективной модели УЭ в своем сознании (тезаурусе обучаемого).

2. Поэтапная реализация алгоритма деятельности по формированию модели УЭ в той или иной знаковой форме (речевой, текстовой и т. д.).

Достаточным условием корректного выбора модели УЭ, соответствующей формулировке поставленной перед обучаемым познавательной задачи, является совпадение всех элементов НС и КС задачи с исходными и конечным элементом модели УЭ. Количество же успешно переработанной обучаемым на данном этапе решения познавательной задачи семантической информации определится суммарной структурной сложностью этих установленных элементарных связей. В соответствии с (2.93-2.96) и (2.98) имеем:

где: - количество исходных и конечного элементов графовой модели (НС и КС предмета познавательной задачи); x(t), y(t) - параметры графовой модели в момент t:

x(t1) = 0, y(t1) = 1

x(t2) = 1, y(t2) = 2

Таким образом, трудоемкость первого этапа определяется количеством семантической информации I1, содержащейся в лесе из n элементарных деревьев, каждое из которых содержит 2 бита информации (информацию об эквивалентности двух понятий, принадлежащих предмету задачи и модели УЭ).

Количество переработанной семантической информации в процессе формирования модели УЭ определим, исходя из следующих соображений:

- информационный поток (2.98) в общем случае носит дискретный характер, определяющийся временем и характером образования связей между семантическими единицами формируемой графовой модели УЭ;

- в момент времени t = 0 начала формирования структуры модели УЭ количество содержащейся в ней семантической информации равно нулю (S = 0), поскольку сама структура еще отсутствует, а количество информации, содержащееся в исходных семантических единицах модели уже учтено на этапе восприятия условий познавательной задачи (2.99).

Тогда:

где: x(tj), y(tj) - параметры графовой модели в момент tj (j = 0,К).

Согласно свойствам определенного интеграла (2.100) можно представить в виде:

где: x(t0), y(t0), x(tк), y(tк) - параметры графовой модели в начальный и конечный момент ее формирования.

Поскольку мы рассматриваем идеальную деятельность обучаемого, то в конечный момент tk количество информации в модели, представленной обучаемым, равно количеству семантической информации (2.93), содержащейся в эталонной модели УЭ. Тогда, решая (2.101) с учетом того, что в начальный момент t0 S(y, V, E) = 0, имеем: