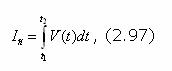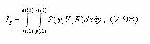Характеристика графовой модели способа решения задачи определения ЭДЦ по данным РЛС

В виде приведенной выше методики мы имеем алгоритм расчета количества семантической информации, содержащейся в эталонной модели УЭ. Этот алгоритм построен на основе данных теории информации, справедлив для широкого класса графовых моделей и полностью базируется на специфических особенностях их структуры. Покажем, что данный алгоритм обеспечивает оценку количества семантической информации, переработанной обучаемым в процессе его учебной деятельности по формированию модели УЭ.

В дидактике существует понятие трудоемкости (объективной сложности) УЭ, употребляемое для объективной оценки его объема и сложности вне связи с потребителем (обучаемым). Трудоемкость УЭ "определяется объемом и логической структурой учебного материала, или, иначе, числом семантических единиц и структурой отношений между ними" [56,С.69]. С другой стороны, трудоемкость учебной деятельности обучаемого по формированию модели УЭ как и любой другой умственной деятельности определяется тем количеством смысловой (семантической) информации, которое необходимо переработать (преобразовать) обучаемому при усвоении им определенного понятия (УЭ), предъявлении усвоенного УЭ обучающему или решении учебной задачи. Определить трудоемкость усвоения УЭ обучаемым можно, используя понятия потока информации и информационного потока:

1. Под потоком информации будем понимать количество семантической информации, формируемое или преобразуемое в единицу времени, тогда

где: V(t) - мгновенное значение потока информации или скорости ее преобразования [бит/сек]; Ic - количество семантической информации, сформированное или преобразованное обучаемым в интервале времени с t1 до t2.

2. Под информационным потоком будем понимать математическую модель изменения параметров (х -ранг связности пучка, у - число элементов) модели УЭ во времени, адекватно отображающую процесс преобразования обучаемым модели УЭ, тогда:

где: x(t1), y(t1), x(t2), y(t2), - параметры формируемой обучаемым графовой модели УЭ соответственно в моменты времени t1 и t2; S(y, V, E) - общее количество семантической информации в том виде графовой модели УЭ, который сформирован обучаемым к моменту времени t.