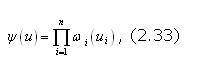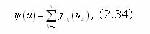| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 245 Условие независимости по предпочтению. Пара показателей (ui,uj) не зависит по предпочтению от остального набора показателей эффективности u(i,j-)=(u1,...,ui-1,ui+1,...,uj-1,uj+1,...,un), если отношение предпочтительности, установленное между векторами uе = (uie,uje,uе(i,j-)) и uk = (uik,ujk,uk(i,j-)) не зависит от уровней, на которых зафиксированы значения показателей u(i,j-). Согласно данному определению из независимости по предпочтению показателей (ui,uj) следует, что, определив отношение предпочтительности на плоскости Ui ´ Uj с учетом только показателей ui и uj, можно распространить найденные отношения предпочтительности на все пространство U. В теории эффективности обосновано, что, если каждая пара частных показателей (ui, uj); i ¹ j; i,j = Формы, эквивалентные аддитивной. Принято, что интегральные критерии j(u) и y(u) эквивалентны, если отношения предпочтительности, определяемые с их помощью между любой парой ue,uk ÎU совпадают. Отсюда следует, что интегральные критерии, получаемые один из другого с помощью монотонных преобразований (функциональных преобразований шкал), эквивалентны. Поэтому аддитивной форме эквивалентны следующие формы представления интегрального критерия: 1. Мультипликативный критерий
логарифмируя который, нетрудно перейти к аддитивной форме. 2. Аддитивные критерии вида где fk - любая из приведенных выше форм функционального преобразования шкалы измерения uk. В теории эффективности разработаны алгоритмы построения всех приведенных выше форм интегрального критерия, подробное описание этих алгоритмов можно найти в [83, С.173-193]. При всех отличиях этих алгоритмов в своей основе они опираются на предположение об измеримости предпочтительности как минимум в интервальной шкале и представляют собой различные способы согласования шкал измерения отдельных показателей эффективности, объединяемых в интервальный критерий. В заключении краткого анализа данных теории эффективности необходимо отметить, что рассмотренные выше задачи обоснования и формулировки необходимой совокупности частных показателей и интегрального критерия эффективности, являются подготовительным этапом к решению основной проблемы этой теории - проблемы изучения закономерностей, устанавливающих зависимость результата функционирования системы от ее свойств и условий функционирования. Эта проблема в теории эффективности и формулируется в виде прямой и обратной задач. Прямая задача формулируется как задача анализа имеемой системы и состоит в оценке результатов ее функционирования в зависимости от свойств системы (управляемые параметры) и условий функционирования (неуправляемые параметры). Обратная задача формулируется как задача синтеза системы и состоит в отыскании такой комбинации ее свойств и условий функционирования, при которых результаты функционирования будут либо заданными, либо оптимальными в смысле принятого критерия эффективности. При этом в обратной задаче до последнего времени рассматривались два относительно самостоятельных класса подзадач: |
Реклама
|
||
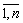 , не зависит по предпочтению от своего дополнения u(i,j-), то интегральный критерий имеет аддитивный вид
, не зависит по предпочтению от своего дополнения u(i,j-), то интегральный критерий имеет аддитивный вид