| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 244 Если выполнены условия существования и непрерывности, то интегральный критерий представим в нормальной форме где u(i) = (u1,...,ui) - вектор, содержащий только первые i из общего числа n показателей. Пусть, например, n = 4, тогда (2.29) примет вид Мультиаддитивная форма. На основе нормальной формы можно получить и другие, более простые по своей структуре представления интегрального критерия формы. Для этого набор используемых показателей эффективности должен удовлетворять дополнительно к условиям существования и непрерывности еще ряду условий. Условие независимости по приращению. Условие независимости по приращению можно сформулировать в компактном виде, введя обозначение для вектора u(i-) = (u1,...,ui-1,ui+1,...,un) не содержащего i-ой компоненты. Показатель ui не зависит по приращению от остальных показателей, если отношение предпочтительности между приращениями этого показателя не зависят от того, на каком уровне зафиксированы значения компонент вектора u(i-). Проверка выполнения условия независимости по приращению для каждого частного показателя эффективности может быть проведена путем установления отношения предпочтительности ЛПР, между одним и тем же приращением Dui показателя ui при различных значениях вектора Если для всех частных показателей u В отличие от нормальной мультиаддитивная форма интегрального критерия представляет собой комбинацию из n функций одной переменной, находить которые, естественно гораздо проще, чем функции многих переменных. Поэтому, когда есть основания полагать, что все критерии независимы по приращению, интегральный критерий целесообразно записывать в мультиаддитивной форме. Аддитивная форма. Дальнейшее упрощение формы интегрального критерия может быть достигнуто только за счет все более сильных условий независимости. Если условие независимости по предпочтению, обеспечивающее возможность представления интегрального критерия в виде аддитивной функции n переменных, рассматривать с этой точки зрения, то его, безусловно, следует признать одним из наиболее ограничительных. |
Реклама
|
||
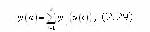

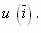 . Если отношение предпочтительности ЛПР к приращению Dui показателя ui сохраняется при любых значениях u(i-), т.е. рост ui равножелателен при любых значениях остальных частных показателей, то показатель Ui независим по приращению.
. Если отношение предпочтительности ЛПР к приращению Dui показателя ui сохраняется при любых значениях u(i-), т.е. рост ui равножелателен при любых значениях остальных частных показателей, то показатель Ui независим по приращению.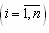 iвыполняется условие независимости по приращению, то интегральный критерий представим в мультиаддитивной форме
iвыполняется условие независимости по приращению, то интегральный критерий представим в мультиаддитивной форме