При построении интегрального критерия целесообразно сначала представить функцию (2.20) как комбинацию других, более простых функций, содержащих меньшее число переменных и потому легче определяемых. В теории эффективности существует много различных способов такого представления, но возможность и корректность использования любого из них определяется требованиями, предъявляемыми ЛПР как к отдельным показателям, так и к их совокупностям, а также спецификой задачи, для решения которой предназначен формулируемый интегральный критерий. В качестве основных форм представления интегрального критерия в теории эффективности рассматриваются следующие формы: нормальная, мультиаддитивная, аддитивная и формы, эквивалентные аддитивной.

Нормальная форма. Представление интегрального критерия в нормальной форме возможно, если он сам и входящие в его состав частные показатели эффективности удовлетворяют условиям существования и непрерывности.

Условие существования. На множестве функций от n переменных y(uj)=y(u1j,...,unj) имеется хотя бы одна такая, что для любых uе, ukÎUn

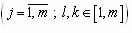
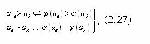
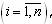Из (2.27) следует, что при выполнении условия существования интегрального критерия набор целей, соответствующих частным показателям uiдля любой j-ой 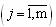рассматриваемой системы, можно заменить эквивалентной этому набору одной количественно измеримой целью. Необходимые и достаточные условия, делающие такую замену возможной, вытекают из (2.2) и формулируются как требование слабого упорядочения к системе предпочтений (2.1), задаваемых ЛПР на множестве сравниваемых систем. Таким образом, если система предпочтений ЛПР является слабо упорядоченной (относится к классу R = IUP отношений слабого предпочтения, допускающего наличие строгих предпочтений P и эквивалентности I), то интегральный критерий существует и, следовательно, задача его нахождения имеет смысл.

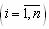Условие непрерывности. Интегральный критерий y(uj) = y(u1j,..., unj) непрерывно дифференцируем в пространстве показателей Uпо всем показателям ui.Это условие в теории эффективности интерпретируется следующим образом.

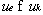Пусть имеются векторы ue,uk Î U,такие, что  причем составляющие их показатели ui 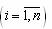удовлетворяют принципу "чем больше, тем лучше". Тогда для любого 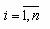вектору uk можно задать приращение i-го показателя Dui > 0, при котором

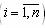Выполнение (2.28) означает, что предпочтения в пространстве U оценок показателей не меняется скачком при изменении этих показателей, а потому малым приращениям Duiпоказателей, должны соответствовать столь же малые приращения интегрального критерия.