| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 242 Оценки систем s1 и s2 доминируют над остальными векторами соответствующих рядов и нет векторов (систем), доминирующих над ними. Вектор системы s7 не доминирует ни над каким из векторов, но и векторы других систем, доминирующие над ним, также отсутствуют. Таким образом, отношение доминирования задает на U частичный порядок и не может быть определено для некоторых uj Î U. Векторная оценка ujÎU, не доминируемая векторами uÎU, называется эффективной на множестве U. Множество Р всех эффективных на U векторных оценок называется эффективной границей множества U или множеством Парето. На рис. 2.1.8 эффективными являются векторные оценки u1, u2, u7 соответственно систем s1, s2, s7. Из этого же рисунка ясно, что оптимальная система s0ÎP={s1, s2, s7}. При этом безразлично, какой разумный смысл вкладывается в понятие оптимальности - so всегда будет принадлежать Р. Верно и обратное: для любой векторной оценки ujÎP можно подобрать разумный принцип оптимальности, по которому uj будет признана u0, т.е. принадлежащей s0 - наиболее предпочтительной системе. Какой из принципов оптимальности в наибольшей мере соответствует B, можно выяснить, только используя дополнительную информацию от ЛПР. Поэтому определение эффективной границы - это максимум того, что можно сделать в условиях многокритериальности, если ЛПР не может или не хочет раскрыть свою систему предпочтений B. В этом случае ЛПР сам анализирует множество P и выбирает из него оптимальную, по его мнению, векторную оценку u0 и соответствующую ей систему s0 без каких-либо формальных оснований. Рис. 2.1.8. Пример отношений доминирования. В теории эффективности сформулирована и доказана следующая теорема, обеспечивающая достаточно простую процедуру определения эффективной границы для целого ряда систем. Если для некоторых l i > 0, то векторная сумма uj является эффективной, где так, чтобы она пересекала множество U. Рис.2.1.9. К определению эффективной границы При увеличении константы c прямая (2.26) будет перемещаться параллельно самой себе, пока не превратится в касательную к границе множества U в точке up. Дальнейшее перемещение прямой (2.6) вверх невозможно и в точке up выполняется условие (2.25). Следовательно, up - эффективная векторная оценка, соответствующая значениям l1=a, l2=b. Повторяя описанную процедуру для всех других возможных соотношений |
Реклама
|
||

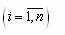
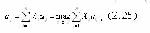
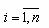 - номер и число частных показателей эффективности, a
- номер и число частных показателей эффективности, a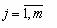 - номер и число рассматриваемых систем. Пусть n=2, а значения весов 1 и 2 фиксированы: l1=a; l2=b. Построим прямую (см.рис.2.1.9)
- номер и число рассматриваемых систем. Пусть n=2, а значения весов 1 и 2 фиксированы: l1=a; l2=b. Построим прямую (см.рис.2.1.9)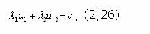
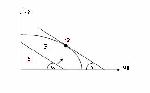
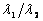 =tga, можно построить эффективную границу P={up}.
=tga, можно построить эффективную границу P={up}.