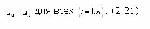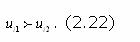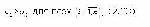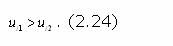В общем виде модели (2.19) обоснования интегрального критерия присутствует параметр m-тип многокритериальной задачи. Наиболее существенным классификационным признаком, определяющим типы многокритериальных задач, является требуемая степень упорядоченности сравниваемых систем. Задачи, требующие полного упорядочения множества S, могут быть гарантированно решены только при условии формулировки интегрального критерия в виде (2.20). К таким задачам относятся задачи оптимизации и ранжировки рассматриваемых систем. В ряде случаев полная упорядоченность систем не требуется: достаточно выделить из S некоторое подмножество наиболее предпочтительных систем. Для этого решают задачи частичного нахождения "удовлетворительных" систем на эффективной границе и задачи нахождения эффективной границы. Последняя задача в отличие от всех остальных не требует выявления B=<Ru>.

Решение задачи нахождения эффективной границы основано на упоминавшемся понятии доминирования. В теории эффективности понятие доминирования имеет следующий формальный смысл [83, C.163-165].

Векторная оценка u1=(u11,..., un1) Î U доминирует над векторной оценкой u2 =(u12,..., un2) Î Un, что записывается как u1 >> u2, если

причем хотя бы для одного i имеет место

Для представительных критериев, удовлетворяющих принципу "чем больше, тем лучше" условия (2.21, 2.22) соответственно имеют вид

причем хотя бы для одного i имеет место

В логическом отношении понятие доминирования представляется бесспорным: если система s1 предпочтительнее системы s2 хотя бы по одному частному показателю эффективности и не уступает (эквивалентна) ей по остальным показателям, то следует признать ее предпочтительность над системой s2. При этом, разумеется предполагается, что используемое для оценки систем множество показателей соответствует полному неизбыточному набору целей нижнего уровня дерева целей. Отношения доминирования, установленные на усеченном множестве показателей, не обязательно сохраняется, а поэтому рассматриваются как некорректные. Использование условий (2.23, 2.24) корректно только для представительных показателей, для косвенных и непредставительных показателей справедливы и корректны соответственно условия (2.12, 2.14).

Используя понятие доминирования, на множествах U, Y и S можно строить ряды доминирования вида u1 >> u2 >> u3..., y1 >> y2 >> y3... или s1 >> s2 >> s3....В этих рядах векторная оценка u1(y1) и соответствующая система s1 доминируют над остальными оценками и системами. На рис. 2.1.8 показаны состоящее из семи векторных оценок множество U и два ряда доминирования заданные на этом множестве для случая, когда i=1,2(n=2), a u1j и u2j соответствуют принципу "чем больше, тем лучше".