| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 239 В теории эффективности наиболее общий вид модели, предназначенной для решения задачи обоснования интегрального критерия (решения проблемы многокритериальности), представлен кортежем где m-тип многокритериальной задачи; S-множество оцениваемых систем, Особенностью использования модели (2.19) является переход из множества S в пространство показателей, более удобное для дальнейшего анализа и установления отношений предпочтительности. Осуществляется этот переход уже рассмотренным выше при изложении основных положений теории шкалирования образом: - для каждого показателя Ui, характеризующего степень достижения одной из частных подцелей системы, определяется вид шкалы, в которой он измеряется, т.е. в L определяется множество Ф={j i} допустимых преобразований ui ® yi; - для каждого из частных показателей ui - с помощью допустимых отображений из L (допустимых функциональных преобразований шкал Li) каждой системе sÎS становится в соответствие вектор оценок y(s)=(y1(s),..., yn(s)), где yi (s) = j[ui(s)] - гомоморфное отображение ui, определяемое видом функции. - определяется вид функции, соответствующей B=< Ru > и позволяющей получить оценку значение M которой, вычисленное для данного вектора y(s); служит оценкой предпочтительности этого вектора и соответствующей ему системы s. В дальнейшем, учитывая однозначное соответствие, установленное между системой s, вектором U(s) и его оценкой y(s) в шкале L, определяемой видом функции, будем оперировать только векторами u(s) или y(s)=j[u(s)] и опускать аргумент s, используя более лаконичные формы записи y=j(u), u=(u1,...un); y=(y1,...yn) там, где это не приводит к недоразумениям. Может оказаться, что вектору uÎU не только не соответствует система из S, но вообще система с такими показателями не существует или нереализуема. В теории эффективности в отношении таких векторов U или их оценок y оперируют, считая их принадлежащими некоторой гипотетической системе. Понятие гипотетической системы очень удобно и широко используется в различных процедурах, направленных на выявление предпочтений ЛПР. |
Реклама
|
||
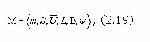
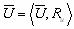 - множество показателей с заданным отношением предпочтения Ru, по которым оценивается система;
- множество показателей с заданным отношением предпочтения Ru, по которым оценивается система; 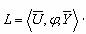 - множество шкал, обеспечивающих измерение всех показателей из
- множество шкал, обеспечивающих измерение всех показателей из 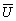 ; B=< Ru > - система предпочтений ЛПР на множестве S; y- решающее правило, задающее на S отношения предпочтительности, удовлетворяющее B.
; B=< Ru > - система предпочтений ЛПР на множестве S; y- решающее правило, задающее на S отношения предпочтительности, удовлетворяющее B.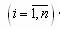 в выбранной для него шкале определяется множество ui его возможных (допустимых) значений, после чего строится пространство допустимых значений критерия эффективности U=U1 ´ U2 ´.... ´Un;
в выбранной для него шкале определяется множество ui его возможных (допустимых) значений, после чего строится пространство допустимых значений критерия эффективности U=U1 ´ U2 ´.... ´Un;