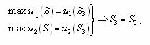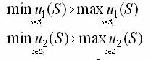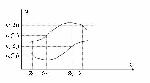
Пусть, например, для оценки систем используются два представительных показателя эффективности u1 и u2, значения которых желательно максимизировать. Множество оцениваемых систем формально задано отрезком оси абсцисс (вещественных чисел) S = [s1, s2]. Характер изменения показателей u1 и u2 на множестве S показан на рис.2.1.7.

В области S2 = [s2,s3] оба показателя u1 и u2 изменяются согласованно: увеличение u1 сопровождается увеличением u2. Поэтому, оптимизируя систему по каждому показателю в отдельности, получим:

т.е. система S3 оптимальна на множестве S2 одновременно по обоим показателям. Таким образом, если показатели эффективности согласованы, для оптимизации системы достаточно использовать один (любой) показатель и "многокритериальная" задача вырождается в однокритериальную. Получить в результате квантификации общей цели А системы набор согласованных частных показателей эффективности - удача столь же большая, сколь и редкая. Как правило, используемые для оценки систем частные показатели противоречивы: повышение значения одного влечет снижение значений другого (других) показателя.

Рис.2.1.7. Характер изменения показателей эффективности на множестве S рассматриваемых систем

На рис.2.1.7 показатели u1 и u2 противоречивы в областях S1 = [s1, s2] и S3 = [s3, s4]. Например, в области S1 для всех Si Î S1, max u1(S) = u1(S2), a max u2(S) = u2(S1) и не существует системы so Î S1, оптимальной одновременно по u1 и u2. Все же можно утверждать, что s0 Î S1:

и поэтому любая система s Î S3 превосходит по обеим частным показателям (доминирует) любую систему s Î S1. Следовательно, если s0 оптимальна на S, то so Î S3. Однако, определить какая из систем из S3 = [s3, s4] оптимальна, на основании только значений u1 и u2, невозможно: на S3 не существует доминирующих систем. Поэтому для нахождения оптимальной системы требуется дополнительная информация о предпочтениях на S3 = [s3, s4], не содержащаяся в самих значениях показателей эффективности u1 и u2, хотя, конечно, связанная с ними.

Необходимость выявления, формализации и учета такой информации возникает всякий раз, когда от частных предпочтений по отдельным показателям эффективности требуется перейти к единому отношению предпочтительности, заданному на всей совокупности противоречивых показателей. Однако оценка систем на множестве противоречивых частных показателей всегда сопряжена с многочисленными трудностями, связанными, в первую очередь, с построением единой шкалы для измерения оценки предпочтительности, позволяющей сопоставлять и сравнивать оценки показателей, имеющих различные размерности и физический смысл. Совокупность этих трудностей и составляет суть проблемы обоснования интегрального критерия.