| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 236 1. Линейная зависимость (линейные преобразования). 1.1. Шкалирование отношений по базовому показателю качества (операция нормирования 1.2. Шкалирование разности по базовому значению показателя качества (операция разности 1.3. Шкалирование отношения по предельно допустимому нижнему отклонению 1.4. Шкалирование отношения отклонений от базового показателя по значению этого базового показателя 1.5. Шкалирование отношения по предельно допустимому верхнему отклонению 1.6. Шкалирование отношения отклонений от верхней (нижней) границы по верхнему (нижнему) предельному отклонению
2.1. Зависимость Харрингтона 2.2. Зависимость Томашевского 3. Ступенчатая зависимость. Ступенчатое преобразование рассматривается как отношение подобия с a = К в области допустимого качества и a = 0 вне ее. При К = 1 соответственно u' = 1 в области допустимого качества и u' = 0 вне ее. Такая мера u' есть селектирующая функция области допустимого качества (рис.2.1.5). 4. Степенная зависимость. Наиболее часто используется в виде Законы функционирования систем класса АС изучены не столь тщательно и полно, чтобы по ним можно было легко определить для сформулированного показателя или критерия класс допустимых преобразований и соответствующий ему вид шкалы. В таких случаях используется следующая общая стратегия: в процессе квантификации сформулированной на качественном уровне общей цели А системы представлять сформулированные на более низком уровне иерархии составляющие ее подцели в более сильной шкале, чем представлена порождающая эту подцель цель более высокого уровня. При этом резкий переход от наиболее слабых шкал к наиболее сильным не рекомендуется, т.к. в результате такого скачка может быть просто не выявлен ряд промежуточных подцелей, оказывающих определяющее влияние на достижение общей цели А системы. Только тщательный анализ в процессе квантификации общей цели системы каждой из получаемых на более низких уровнях иерархии подцелей, проводимый вплоть до выявления на низшем уровне этой иерархии полного неизбыточного набора количественно измеримых целей и соответствующих им наборов физически измеримых параметров (характеристик) системы, которые могут быть приняты в качестве частных показателей эффективности, а также последующая оценка представительности этих показателей на основе выявления мнения ЛПР обеспечивают определение полного неизбыточного набора количественно измеримых показателей эффективности системы, с необходимой степенью доверия отображающих соответствие системы целевому назначению. |
Реклама
|
||
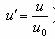 ). Применяется при построении относительных показателей качества (рис.2.1.3, а).
). Применяется при построении относительных показателей качества (рис.2.1.3, а).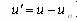 ). Применяется для построения разностных показателей, характеризующих отклонение от базового значения, рассогласование с ним (рис.2.1.3, б).
). Применяется для построения разностных показателей, характеризующих отклонение от базового значения, рассогласование с ним (рис.2.1.3, б).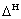 разностного показателя
разностного показателя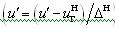 .Применяется для показателей, имеющих одностороннюю нижнюю границу. В области допустимого качества 0 £ u’< +¥, вне области u’< 0 (рис.2.1.3 в).
.Применяется для показателей, имеющих одностороннюю нижнюю границу. В области допустимого качества 0 £ u’< +¥, вне области u’< 0 (рис.2.1.3 в).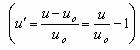 . Характеризует относительные рассогласования, отклонения (рис.2.1.3, г).
. Характеризует относительные рассогласования, отклонения (рис.2.1.3, г).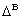 разностного показателя
разностного показателя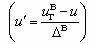 . Применяется в для односторонних убывающих показателей. В области допустимого качества 0£ u’<+¥, вне области u' < 0 (рис.2.1.3, д).
. Применяется в для односторонних убывающих показателей. В области допустимого качества 0£ u’<+¥, вне области u' < 0 (рис.2.1.3, д).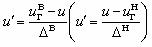 . Применяется для односторонних убывающих (возрастающих) показателей качества (рис.2.1.3,е).
. Применяется для односторонних убывающих (возрастающих) показателей качества (рис.2.1.3,е).
 2. Экспоненциальная зависимость. В основном применяется два типа экспоненциального шкалирования относительного разностного показателя качества:
2. Экспоненциальная зависимость. В основном применяется два типа экспоненциального шкалирования относительного разностного показателя качества: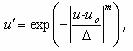 , где
, где 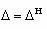 для u<uo,
для u<uo, 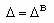 для u>u0. В области допустимого качества
для u>u0. В области допустимого качества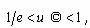 , вне области
, вне области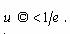 . Мера u’ имеет максимум при базовом значении показателя u0. ( рис.2.1.4,а).
. Мера u’ имеет максимум при базовом значении показателя u0. ( рис.2.1.4,а).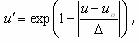 , где
, где 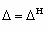 для u<uo,
для u<uo, 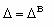 для u>u0. В области допустимого качества 1<u’< e, а вне ее u’< 1. (рис.2.1.4. б).
для u>u0. В области допустимого качества 1<u’< e, а вне ее u’< 1. (рис.2.1.4. б).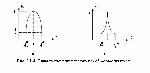
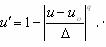 . Область допустимого качества симметрична и характеризуется значением меры 0 £ u’£ 1 (рис.2.1.6).
. Область допустимого качества симметрична и характеризуется значением меры 0 £ u’£ 1 (рис.2.1.6).