| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 232 2. Квазипорядок - если есть хотя бы одна пара равноценных элементов, т.е. есть хотя бы одна пара встречных дуг на диаграмме ориентированного графа. Определения строгого, нестрогого линейного и частичного квазипорядка соответствуют аналогичным определениям порядка. В отличии от рассмотренных выше неметризированных (качественных) отношений в случае установления метризованных отношений указывается не только факт выполнения отношения u(si)Ru(sj), но также и степень количественного превосходства: "на сколько u(si) предпочтительнее u(sj)" (аддитивное метризованное отношение) или "во сколько раз u(si) предпочтительнее u(sj)" (мультипликативное метризованное отношение). На основе анализа вида отношений между рассматриваемыми элементами u(si) устанавливается тип порядка, заданного на эмпирической системе, что позволяет научно обоснованно и правильно выбрать тип шкалы для измерения исследуемого качества (параметра) u(si), характеризующего рассматриваемую систему. В квалиметрии процесс измерения рассматривается как процесс отображения реальной эмпирической системы в ее концептуальную (абстрактную) модель, представляющую собой знаковую образную (неязыковую) или числовую (языковую) систему. Измерение эмпирической системы U={ui} (ui используется вместо u(si) для простоты обозначения), на которой установлено отношение Ru, состоит в определении знаковой системы Y={yi} между элементами которой установлены отношения Ry, адекватные отношению Ru на U. Соответствие между Шкалой в современной теории измерений называют кортеж из трех элементов Такое определение охватывает как количественные, так и качественные шкалы. Иерархическая структура основных шкал приведена на рис. 2.1.2. К качественным и слабым шкалам относят номинальную шкалу, шкалу порядка (ранговую шкалу) и шкалу гиперпорядка. К количественным и сильным шкалам в свою очередь принадлежат: степенная шкала и шкала интервалов; логарифмическая шкала, шкала разностей и шкала отношений, а также абсолютная шкала. Функция, входящая в определенные шкалы, не является единственной. Множество Ф={ji} - множество допустимых преобразований ui ® yi - является одной из главных характеристик шкалы. |
Реклама
|
||
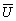 = {U, Ru} и
= {U, Ru} и 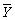 ={Y, Ry} устанавливается с помощью гомоморфного отображения, такого, что (j (u1), j(u2)) Î Ry Û (u1, u2) Î Ru, где символ Û означает "тогда и только тогда, когда". Качественные (неметризованные) предпочтения Ru на множестве U´U в результате измерения переводятся в знаковые (в том числе и количественные) отношения Ru на множестве Y´Y.
={Y, Ry} устанавливается с помощью гомоморфного отображения, такого, что (j (u1), j(u2)) Î Ry Û (u1, u2) Î Ru, где символ Û означает "тогда и только тогда, когда". Качественные (неметризованные) предпочтения Ru на множестве U´U в результате измерения переводятся в знаковые (в том числе и количественные) отношения Ru на множестве Y´Y.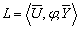 , а процесс измерения представляют как отображение множества элементов эмпирической системы на числовую ось Rе:
, а процесс измерения представляют как отображение множества элементов эмпирической системы на числовую ось Rе: