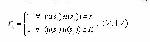Пусть некоторая эргономическая характеристика (характеристика антропотехнической системы) может быть представлена в виде ряда альтернатив u(s1), u(s2)... u(sn), в совокупности образующих некоторое множество неупорядоченных элементов U={u(si)}. В зависимости от условий конкретной задачи между этими элементами могут быть заданы отношения (2.1) предпочтения. Задание таких предпочтений превращает неупорядоченный набор элементов в упорядоченный - в множество с заданными отношениями, называемое в квалиметрии моделью. Наиболее часто встречающимися и достаточно хорошо изученными являются бинарные отношения.

Если задано множество U={u(si)}, то множество пар вида (u(si) u(sj)) с элементами u(si)ÎU и u(sj)ÎU образует прямое (декартово) произведение U´U. Любое подмножество К декартова произведения называется бинарным отношением на множестве U. В состав этого подмножества К включают только те пары. для которых определено заданное предпочтение R из (2.1).

Информация о неметризованных (качественных, неколичественных) отношениях может быть представлена в следующих видах:

- непосредственным перечислением пар элементов, принадлежащих подмножеству К;

- в виде графа, вершины которого соответствуют элементам множества U, а ориентация ребер соответствует заданному ему отношению R;

- в виде матрицы с элементами rij, которые задаются в следующем виде:

Как указывалось выше, на одном и том же множестве U можно задать различные отношения из (2.1) и получить в зависимости от специфики U различные степени упорядочения

u(Si) Î U: от групп несвязных элементов до строго упорядоченной последовательности элементов. Степень этой упорядоченности определяется содержательной стороной отношений R из (2.1) и спецификой множества U как отображения множества S={si}.

В теории бинарных отношений порядки на неметризованных элементах множества К задаются с помощью указания наличия наборов из следующих свойств:

1. Рефлективность. Отношение R называется рефлексивным, если пары (u(si), u(sj))ÎR для всех iÎ{1, 2,... n}. Примеры рефлексивных отношений: "не больше", "не меньше", "быть похожим на" и т.д.

2. Антирефлексивность. Отношение R называется антирефлексивным, если пары (u(si) u(sj))ÏR для всех iÎ{1, 2,... n}. Примеры антирефлексивных отношений: "больше", "меньше", "не иметь ни одного общего признака".