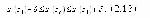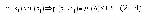Большинство критериев, используемых на практике, являются косвенными. Из (2.8) и графика на рис.2.1.1 следует, что для косвенных критериев;

Согласно (2.12), косвенный критерий реализует принцип: с вероятностью не меньшей чем m(d), большему значению критерия соответствует лучшая (худшая) система. Косвенный критерий в определенной мере отражает отношения предпочтительности, установленные ЛПР на множестве S. Однако связь между этими отношениями и значениями критерия носит не функциональный, как у представительных критериев, а вероятностный характер. Это существенно усложняет интерпретацию результатов сравнения систем по косвенным критериям. Так, если для системы Si имеем отношение (2.11) по косвенному критерию, то отсюда можно сделать лишь заключение, что с вероятностью m(d) оптимальная система So имеет значение критерия, заключенное в интервале

Если ЛПР величина вероятности m(d) покажется недостаточной для принятия решения о выборе оптимальной системы, она может быть увеличена за счет введения дополнительных показателей, характеризующих ту же самую цель, что и исходный критерий. В [83, С.153-155] сформулирован следующий подход к формированию набора (вектора) косвенных показателей (критериев), характеризующих данную цель:

1. Выявляется множество U всех показателей ui(S), по которым можно судить о степени соответствия системы цели А.

2. Для каждого показателя ui Î U, найденного на первом этапе, определяются величины di и значение mi(di). Кроме того задают величину mo - нижнюю границу представительности, необходимой ЛПР для принятия решения о выборе лучшей системы.

3. Показатели ui Î U располагаются в порядке убывания значений mi(di), после чего им присваиваются новые номера так, чтобы i< j Þ mi(di)³ mj(dj).

4. Из полученной последовательности векторов формируются следующие показатели:

u1=u1, u12=(u1,u2), u123=(u1, u2, u3) и т.д.

Затем с помощью ЛПР определяют значения представительности m1(d1), m12(d12) и т.д. На n-ом шаге оказывается, что для вектора un=(u1... un) величина mn(dn) > mo. Тогда un - вектор показателей наименьшей размерности, позволяющий производить оценку отношений предпочтительности систем с требуемой представительностью принимается в качестве критерия эффективности.

При сравнении систем si,sjÎS, отличающихся по значению U(S) на величину d (см.рис.2.1.1), для непредставительного критерия имеем:

При m(d)=0,5 критерий не несет никакой информации об отношении предпочтительности систем sÎS. Из (2.14) следует, что при m(d)=0,5 p(si R sj) = p(sj R si) =0,5. В случае, если