| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
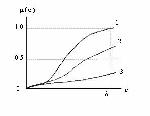
Стр. 227 Далее существует разделение критериев на представительные, косвенные и непредставительные критерии. Пусть d - минимальное значение e, принимаемое во внимание ЛПР при установлении отношений (2.1) предпочтительности между системами siÎS. Величина d определяется исходя из конкретной ситуации, но в любом случае d > 0. Так, если значения U(S) получают измерением с помощью прибора, цена деления которого равна g, то, как известно, точность измерения не может превосходить величины d=0.5 g. Когда множество S дискретно для всех sÎS принимают При этом ЛПР не встретится с необходимостью рассматривать системы, для которых разность значений критерия меньше величины (2.6). Если S - непрерывное множество, а значения критерия для всех sÎS определяются расчетным путем, то величина d должна соответствовать погрешности принятых формул и используемых в расчете данных. Критерий U(S), определенный на множестве сравниваемых систем S называется представительным, если при e ® d косвенным, если при e ® d и непредставительным, если при e ® d Каждый из перечисленных видов критериев обладает своей спецификой, диктующей различные подходы к их использованию для сравнительной оценки систем по предпочтительности. Графики функций доверия всех трех видов критериев представлены на рис.2.1.1. Как указывалось выше, для любой sÎS величина e ³ d. Тогда непосредственно из графика для представительного критерия очевидно следующее выражение: где под отношением R понимается либо Отсюда для представительного критерия следует, что для любых s Î S и процедура оптимизации системы эквивалентна отысканию экстремума U(S), что является чисто формальной задачей, имеющей многочисленные и хорошо развитые методы решения. Рис.2.1.1. Функции доверия представительного (1), косвенного (2) и непредставительного (3) критериев Условие (2.11) показывает, что представительный критерий реализует выполнение четкого и простого принципа: большему значению критерия соответствует лучшая (худшая) система. Справедливым считается и обратное утверждение: если данный принцип выполняется, то рассматриваемый критерий является представительным. Четкость и простота процедуры (2.11) оптимизации создают естественный соблазн оперировать со всеми критериями как с представительными. Однако, это удается не часто, поскольку наличие представительного критерия по существу означает, что для сложного качественного понятия цели А удалось дать адекватное количественное описание (критерий). |
Реклама
|
||
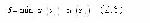
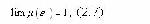
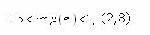
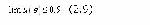
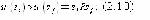
 либо
либо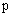 .
.