Стр. 88
Психология указывает два пути формирования полноценных понятий: 1) варьирование объектов (изменение как существенных, так и несущественных признаков); 2) вооружение учащихся при изучении какого-либо понятия ориентировочной основой действий с этим понятием для решения соответствующих задач. “Обобщение всегда идет лишь по тем предметам, которые вошли в состав ориентировочной основы действий, направленных на анализ этих предметов” [146, С.77]. Поэтому, скрывая от учащихся в задачах условие, действия или ответ, можно оказывать влияние на развитие определенных, “западающих” у конкретного учащегося логических операций.
Комбинируя известные и неизвестные компоненты – условия (У), действия (Д) и ответ (О) – можно теоретически получить несколько типов задач (см. таблицу 2.1. - 1). Рассмотрев основные признаки, значение и роль, которую играют приведенные типы задач в развитии мышления и компонентов познавательной самостоятельности старшеклассников, мы сможем ответить на вопрос о том, задачам какого типа как средству развития операционных умений и навыков ведения самостоятельной познавательной деятельности необходимо отдать предпочтение.
Таблица 2.2.1 – 1. Классификация учебных задач по наличию структурных компонентов
Тип задачи
| Наличие компонентов задачи
| Характеристика типа задач
| Примеры задач
|
1
| 2
| 3
| 4
|
1.
| У Д О
| Задачи-примеры в текстах параграфов.
| |
2.
| У Д ?
| Математические задачи на отбор правильного ответа.
Дан алгоритм. Определить результат его исполнения.
| Модификация текста задачи
[52, С.207].
Решим уравнение 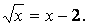
Возведя в квадрат обе части уравнения, получим 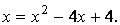 После преобразований приходим к квадратному уравнению После преобразований приходим к квадратному уравнению 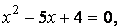 корни которого корни которого 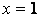 и и 
Из полученных решений отберите числа, являющиеся корнями исходного уравнения.
Чему будут равны переменные А$ и B$ после выполнения следующей программы?
10 A$=“РАДИО”
20 B$=“ВЕЩАНИЕ”
30 B$=A$+B$
40 A$=MID$(B$,3,3)+MID$(A$,3,1)
50 B$=MID$(B$,1,1)+MID$(B$,5,1,) + MID$(B$,8,2)
60 STOP
[26, С.189].
|
3.
| ? Д О
| По данному решению и ответу составить задачу.
По готовой программе и ответу выяснить первоначальные соотношения данных условия.
| Для приведенного решения сформулируйте условие с практическим содержанием.
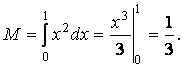
Ответ: 1/3.
Определите назначение программы и сформулируйте задание с практическим содержанием, требующее приведенного решения.
“5 DEF FNF(x)=X^3-3*X-3
10 A=0
20 B=1
30 INPUT E
40 C=(A+B)/2
50 IF FNF(C)=0 THEN 90
60 IF FNF(A)*FNF(C)<0 THEN C=B ELSE C=A
70 IF ABS(B-A)>E THEN 40
80 C=(A+B)/2
90 ? “Корень Х=“; С; “ при Е=“; Е
100 END
run
Корень Х=0.9995118 при Е=0.001”
|
4.
| У ? О
| Большинство задач школьного курса математики.
| |
5.
| У ? ?
| Задачи школьных курсов математики и информатики.
При условии, что конкретные данные не указаны или скрыты связи между данными – это задачи, требующими для своего решения построения некоторой модели.
| Из всех прямоугольников, вписанных в окружность, найдите прямоугольник наибольшей площади [1, С.155].
“Известны данные, показывающие продолжительность горения (в часах) электрических ламп, изготовленных на двух заводах. (Даны числовые значения.) Можно ли утверждать, что на заводах поддерживаются одинаковые технологические условия производства?” [26, С.173]
|
6.
| ? Д ?
| По данному алгоритму решения задачи получить данные, провести анализ и записать ответ. Обобщив результаты, составить условие.
| Дан алгоритм:
Написать все натуральные числа
от 2 до n.
Пока есть необведенные числа среди невычеркнутых, повторять:
Среди невычеркнутых чисел обвести наименьшее из необведенных.
Из необведенных чисел вычеркнуть те, которые кратны последнему обведенному числу.
Конец цикла.
а) Выполните алгоритм при n=6, 12, 100. Какие числа будут обведены после окончания выполнения алгоритма в каждом из этих случаев?
б) Для решения какой задачи предназначен этот алгоритм? Обоснуйте ответ.
Подметьте закономерность и сформулируйте свойство показательной функции y=ax, отражающее поведение графика функции в зависимости от значения основания а. На основании полученного свойства схематично изобразите графики функций y=10х и y=(1/2)x.
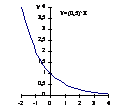 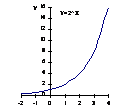 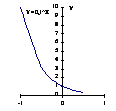 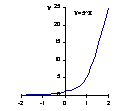
|
7.
| ? ? О
| Конечный результат, ответ, известен, исходные данные – условие и действия, отражающие связи между исходными (доступными) данными и результатом – требуется определить.
| Выясните свойства функции y=ex.
Смоделировать на экране ЭВМ полет мяча, брошенного под углом к горизонту.
|
1-й тип. Объяснительно-иллюстративные или репродуктивные задачи. Ученик знает, из чего надо исходить, какие действия необходимо выполнить, каких результатов надо достичь. Функции учащегося в обучении сводятся к тому, чтобы проанализировать, запомнить предлагаемый материал и в должный момент воспроизвести его. Все мыслительные операции задействованы, в основном, на этапе запоминания и воспроизведения материала (содержание, действие, ответ задачи). Примеры таких задач – задачи, приводимые авторами учебников в текстах параграфов.
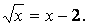
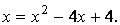 После преобразований приходим к квадратному уравнению
После преобразований приходим к квадратному уравнению 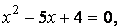 корни которого
корни которого 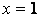 и
и