| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Пустовойтов В.Н. Развитие познавательной самостоятельности учащихся старших классов (на материале математики и информатики) : дис.... канд. пед. наук : 13.00.01 : защищена 25.06.02 : утв. 22.11.02. –– Брянск, 2002. – 205 с.
Стр. 132 Имеем Ответ: -1.” 2-я группа. Задача №1. Какие из чисел 2, 1, -1, 0, -2 являются корнями уравнения Задача №2. Закончите решение Задача №3. Верно ли начато решение уравнения Вычислите корни данного уравнения. Задача №4*. Введя новую переменную, решите уравнение 3-я группа. Задача №1. После возведения в квадрат обеих частей иррационального уравнения было получено следующее равенство: 3x2+6x+1=49-14x+x2. Восстановите первоначальный вид уравнения и решите его. Задача №2. Задача №3. Воспользуйтесь равносильным переходом Задача №4*. Решите уравнение 4-я группа. Задача №2. На основании определение арифметического квадратного корня при решении иррационального уравнения была получена система Задача №3. Некоторое иррациональное уравнение решали методом подстановки (введена новая переменная y) и получили следующую запись: Восстановите исходный вид этого уравнения и решите его другим методом. Задача №4*. Решите уравнение наиболее рациональным методом 5-я группа. Задача №1. Решите уравнения, выбирая наиболее рациональные методы решений: а) в) Задача №2. Составьте уравнение, соответствующее равносильному переходу в своем решении к системе Обобщение. Подведение итогов. Для подведения итогов урока представителям групп предлагается выписать на доске методы решения иррациональных уравнений, примененные учащимися в ходе работы, и соответствующие примеры. После выступлений старшеклассников, учителем делается обобщение, выделяя следующие пять методов решения иррациональных уравнений: |
Реклама
|
||
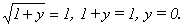 Откуда
Откуда 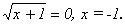
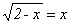 ?
?
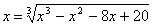 ?
?
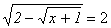 .
.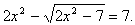 Какой из методов решения для данного уравнения наиболее рациональный а) метод возведения обеих частей в квадрат или б) метод подстановки?
Какой из методов решения для данного уравнения наиболее рациональный а) метод возведения обеих частей в квадрат или б) метод подстановки?
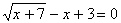 .
.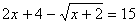 .
.
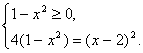 Восстановите первоначальный вид уравнения и решите его.
Восстановите первоначальный вид уравнения и решите его.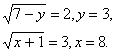
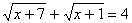 . Указание: используйте умножение на сопряженное выражение.
. Указание: используйте умножение на сопряженное выражение.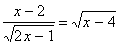

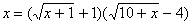 .
.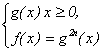 . Решите составленное уравнение.
. Решите составленное уравнение.