Ход урока

Организационный момент

Учащим сообщаются цели и задачи предстоящей работы: повторить способы решения иррациональных уравнений, научиться по виду уравнения отбирать оптимальные способы решения.

Актуализация знаний. Проверка выполнения заданий домашней работы.

На этом этапе рассмотрены варианты выполнения учащимися заданий домашней работы и фронтально разобраны задания:

а) Какие из следующих уравнений являются иррациональными:

?

Дайте определение иррационального уравнения.

б) Найдите область определения функций:

.

в) Не решая следующих уравнений, объясните, почему каждое из них не может иметь корней:

.

Самостоятельная работа учащихся в группах

Учащиеся разбиваются на группы. Каждой группе предлагается к решению ряд заданий, дифференцированных по сложности. В ходе работы учителем оказывается дозированная помощь.

Дифференцированность заданий способствовала тому, что практически все учащиеся могли самостоятельно их выполнить. Тем самым, выполняя работу, старшеклассники приобрели положительный эмоциональный опыт самостоятельной познавательной деятельности. Задания требуют переноса теоретических знаний на практику, способствуют формированию умений проводить отбор наиболее рациональных методов решения. Выполнение ряда заданий предполагало обращение учащихся к справочной литературе по методам решения уравнений и систем уравнений, что также способствовало формированию и совершенствованию умений старшеклассников ведения самостоятельной познавательной деятельности.

Группам были предложены следующие задания.

1-я группа.

Задача №1. Возведя обе части уравнения в квадрат, решите уравнение .

Задача №2. Закончите решение уравнения

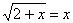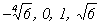Задача №3. Какие из чисел являются корнями уравнения 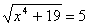? Имеет ли данное уравнение еще корни?

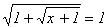Задача №4*. Проверьте, верно ли решено уравнение ?

“Подстановка: