Задания группе
| Вариант помощи
|
1. Величина вклада в коммерческом банке описывается таблицей:
| |
| | | | | | | | | | |
Месяц
| 1
| 2
| 3
| 4
| 5
| ...
| | | |
Величина вклада
(в тыс.руб)
| 2
| 4
| 8
| 16
| 32
| ...
| | | |
Определить, какой функцией описывается рост вклада?
Какова будет сумма вклада через год?
Дайте определение показательной функции.
| Установите, какова зависимость между величиной вклада и порядковым номером месяца.
Функция, заданная формулой ..., называется показательной функцией с основанием ...
|
2. С помощью ЭВМ постройте графики функций y=2x, 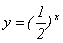 , y=5x, , y=5x, 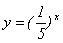 , y=3,5x, , y=3,5x, 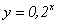 . .
Сделайте схематичные рисунки графиков в тетрадь.
Обратите внимание на поведение графиков в зависимости от основания.
Сделайте вывод, заполнив пропуски в предложении:
“При a ... показательная функция возрастает на всей своей области определения, при a ... показательная функция убывает.”
| Прочитайте пункт учебника.
|
3. Какова область определения и область значений показательной функции.
“Область определения показательной функции у=ах D(y)=...“
“Область значений показательной функции у=ах E(y)=... “.
| Выясните, какие значения может принимать:
переменная X,
переменная Y?
|
4. На основании полученных свойств схематично изобразите графики функций y=6,77х и y=0,1x.
| Обратите внимание на основание степени.
|
5. Для показательной функции остаются верными пять свойств степени, рассмотренные нами на прошлых уроках. Вспомните и запишите их.
| |
6. Какой формулой задается данный график показательной функции?
| Воспользуйтесь свойством степени a1=a.
|
7. Пользуясь свойствами показательной функции (убывание и возрастание функции в зависимости от значения основания а, свойства степени), сравните числа: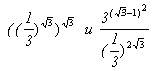 . .
| Воспользуйтесь свойствами
(am)n=amn, .
|
8.* Какому из промежутков (-¥;0), (0;1), (1; +¥) принадлежит корень уравнения 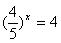 . .
| |
| | | | | | | | | | |
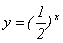 , y=5x,
, y=5x, 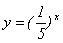 , y=3,5x,
, y=3,5x, 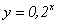 .
. 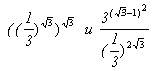 .
.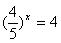 .
.