Последующая группа заданий направлена на формирование умений и навыков по применению полученных теоретических знаний к решению задач. На этом этапе преимущественно используются “задачи с измененной структурой условия”

Задания 1-й группе

(очень низкий уровень познавательной самостоятельности)

Задания группе	Вариант помощи
1. Со времени наблюдения численность бактерий (в миллионах) со временем (в час) изменяется по закону y=2t . Определить, сколько бактерий было в конце 1-го, 2-го, 3-го, 4-го, 5-го часа наблюдения. Сколько миллионов бактерий будет в конце 10-го часа наблюдений? Дайте определение показательной функции. Уточните данное Вами определение показательной функции по учебнику.	Подставьте значение переменной t в данную формулу. Функция, заданная формулой ..., называется показательной функцией с основанием ...
2. С помощью ЭВМ постройте графики функций y=2x, y=5x, y=3,5x. Сделайте схематичные рисунки графиков в тетрадь. Что общего в поведении всех трех графиков (возрастают или убывают)? Какие основания степени у этих функций? Постройте графики функций 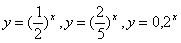. Сделайте схематичные рисунки графиков в тетрадь. Что общего в поведении этих трех графиков (возрастают или убывают)? Какие основания степени у этих функций? Сделайте вывод, заполнив пропуски в предложении: “При a ... показательная функция возрастает на всей своей области определения, при a ... показательная функция убывает.”	Прочитайте пункт учебника.
3. Анализируя полученные графики, сделайте вывод об области определения и области значений показательной функции. “Область определения показательной функции у=ах D(y)=... “. “Область значений показательной функции у=ах E(y)=... “.	Выясните, какие значения может принимать: переменная X, переменная Y?
4. На основании полученных свойств схематично изобразите графики функций y=4х и y=(1/3)x	Обратите внимание на основание
5. Пользуясь свойствами показательной функции (убывание и возрастание в зависимости от значения основания а), проверьте истинность выражений: .	Воспользуйтесь схематичными графиками показательной функции.
6. Решите №449 а),б)
7*. Какому из промежутков (-¥;0), (0;1), (1; +¥) принадлежит корень уравнения 3х=3,5.

Задания 2-й группе