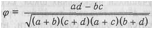Полезно знать, что коэффициент хи-квадрат и коэффициент четырехпольной корреляции взаимосвязаны и, поскольку известна численность и распределение сопоставляемых выборок, указанные коэффициенты могут быть определены один через другой.

Как показывает само название этого метода, числовой материал, подлежащий статистическому анализу, может быть распределен в таблице-графике, имеющей четыре поля. Такое расположение материала облегчает все последующие действия с ним. Чтобы рассмотреть технику вычисления коэффициента четырехпольной корреляции — он обозначается символом <р (фи), — можно воспользоваться тем примером, где речь шла о вычислении коэффициента х2- Выпускники двух школ сравнивались между собой по подготовленности к вузовским экзаменам.

Заменив буквенные обозначения числами, получим:

Для получения коэффициента х нужно воспользоваться формулой х2 = <Р'П. В данном примере х2 = 0,342-187 = 0,1156-187 = = 21,7. Этот же коэффициент х2 вычислялся другим приемом. Получено значение 21,9. Расхождение вызвано разницей в технике вычислений.

Коэффициент четырехпольной корреляции <р может принимать значения от 0 до 1, причем знак получаемого (р не принимается во внимание.

Психологу, намеренному воспользоваться для статистического анализа своих материалов методом хи-квадрат, нужно знать о некоторых обязательных требованиях этого метода; о них не упоминалось в приведенных примерах. При вычислении коэффициента х2 необходимо брать для анализа только абсолютные численности выборок, но не относительные, в частности, не проценты. Необходимость учитывать это свойство объясняется тем, что значение коэффициента х2 зависит от абсолютных величин рассматриваемых распределений. Так, сравнение выборок с численностями 60 и 40 даст совершенно не тот результат, что сравнение выборок с численностями 6 и 4, хотя процентное отношение распределений в обоих случаях одинаково (60 и 40%).