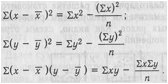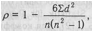Для упрощения расчетов введены некоторые тождества.

Число степеней свободы fd = п - 2 = 15-2= 13. По таблице уровней значимости находим, что при 13 степенях свободы /0,999 ^ = 0,760. Сравниваем это значение с полученным коэффициентом: ^ 0,76 < 0,96.

Полученный коэффициент корреляции показывает, что между ре->, зультатами в тестах «Аналогии» и «Классификации» имеется связь.. Высокий уровень значимости свидетельствует о том, что эта связь с-; высокой вероятностью будет воспроизводиться в таких же экспериментах.

Вычисление коэффициента корреляции по Спирмену! (коэффициент ранговой корреляции).

Исследовательское задание указано на с. 266. Формула ранговой' корреляции такова:

где d — разность рангов ряда х и ряда у т.е. (Rx - Ry).

fd = n - 2 = 15 - 2 = 13.

Производится раздельное ранжирование ряда х и ряда у. Вычисляется разность рангов d попарно. Знак разности не существенен, так как по формуле нужно возвести d в квадрат. Далее действия определяются формулой:

По таблице уровней значимости р > ро,99 (0,98 > 0,70).

Коэффициенты, вычисленные двумя разными способами, как и нужно было ожидать, чрезвычайно близки друг к другу; отличаются они на 0,02, что никакого значения практически не имеет.

Нельзя трактовать коэффициент корреляции как величину, означающую процент взаимозависимых связей вариант двух коррелируемых рядов, т.е. например, коэффициент 0,50 трактовать как 50% таких связей этих рядов. Это далеко не так. Об этом проценте вообще по коэффициенту корреляции судить нельзя. Возведенный в квадрат коэффициент корреляции называется коэффициентом детерминации (г2 или р2). Он показывает, сколько процентов вариант обоих рядов оказались взаимозависимыми. При коэффициенте 0,50 процент таких взаимозависимых вариант составит О,5О2, т.е. 0,25 (Heinz A., Ebner С. Grundlagen der Statistik fur Psychologen, Padagogen und Soziologen. Berlin, 1967. S. 112). Для коэффициента 0,98 коэффициент детерминации составит 0,982 = 0,9604. Следовательно, взаимозависимы примерно 96% вариант обоих рядов.