| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Перова М.Н Методика преподавания математики в специальной (коррекционной) школе VIII вида — М.: Гуманит. изд. центр ВЛАДОС, 2001. —— 408 с.: ил. — (Коррекционная педагогика)
Стр. 126 Запишем 1 — 1=0 (отсутствие предметов обозначают цифрой 0). Решаются еще примеры, когда разность равна ОС^ Нуль сравнивается с единицей. Устанавливается, что нуль меньше единицы, а единица больше нуля, поэтому нуль должен стоять перед единицей. Однако учитель должен помнить, что нуль не относится к натуральным числам. Поэтому ряд натуральных чисел должен начинаться с единицы. Вводить число нуль (0) в качестве вычитаемого, а потом и слагаемого следует на большом числе упражнений. Смысл действий с нулем будет лучше понят учащимися, если нуль в качестве вычитаемого и нуль в качестве слагаемого будет вводиться неодновременно. Затем проводятся упражнения на дифференциацию примеров, в которых нуль будет слагаемым и вычитаемым. Упражнения на дифференциацию должны включать все возможные сочетания, например: 1 — 1, 2—2, 5—5, 1—0, 2—0, 3—0, 1+0, 0+3, 0+0, 0-0 и т. д. В 1-м классе после знакомства с числами от 1 до 5 учитель использует в своей речи названия компонентов и результата действия сложения. Закреплению действий сложения и вычитания способствуют составление примеров с данным ответом на сложение и вычн такие (например Полезно показать учащимся и зависимость изменения сум мм от изменения слагаемых, а также изменения остатка от изменении уменьшаемого. Учитель должен обращать внимание учащихся на то, что сумма всегда больше каждого из слагаемых (или равна ему), а остаток всегда меньше уменьшаемого (или равен ему). Уменьшаемое больше или равно вычитаемому, в противном случае вычитание произвести нельзя. Примеры с тремя компонентами следует сопоставлять с примерами, имеющими два компонента, выявлять их различие. Учителю следует помнить о том, что умственно отсталые первоклассники примеры с тремя компонентами часто решают так же, как с двумя, т. е. выполняют одно действие и сразу записывают ответ, считая, что решение примера закончено, например: 4+2—3=6. Предупреждению подобных ошибок способствует приучение учащихся к планированию предстоящей деятельности. Этому способствует постановка перед выполнением арифметических действий вопросов вида: «Прочитай пример. Сколько действий надо выполнить? Какое 1-е действие? Какое 2-е действие?» Затем требовалось от учащихся рассказать последовательность предстоящих операций. Например: «В примере надо сложить (прибавить) и вычесть. Сначала я буду складывать (прибавлять), потом вычитать, запишу ответ». Можно разрешить на первых порах писать результат первого действия над знаком действия, например: 5+4—2 = 7. Это один из приемов самоконтроля, к которому следует готовить учащихся с 1-го класса. Они должны приучаться к проверке правильности решения примеров. |
Реклама
|
||
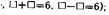 разложение любого числа на два слагаемых (например, 8=... + ..., 10=... + ...); дополнение любого однозначного числа до данного числа или до 10.
разложение любого числа на два слагаемых (например, 8=... + ..., 10=... + ...); дополнение любого однозначного числа до данного числа или до 10.