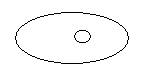
1.2 Теория множеств

1.2.1 Множество. Отношения между множествами

Множество – одно из основных математических понятий. Множество ассоциируется с понятием группа. Множества могут быть конечными, бесконечными, пустыми.

Пустым называется множество, которое не содержит ни одного элемента (Æ).

Множества обозначаются большими буквами латинского алфавита А, В, С,…, а элементы - маленькими буквами а, в, с, ….х, у.

«Элемент а принадлежит множеству А» записывают так: а Î А, если не принадлежит – то в Ï А.

Способы задания множества:

1) путем перечисления всех элементов А = {а, с},

2) путем задания характеристического свойства.

Характеристическое – такое свойство, которым обладает каждый элемент данного множества, и не обладают элементы, не принадлежащие данному множеству.

Например, «натуральные числа больше 3» можно задать так:

А = {n ÎN, n >3}.

Отношения между множествами

Множества изображаются на плоскости с помощью кругов Эйлера.

1. Отношение равенства

Говорят, что А=В, если все элементы множества А принадлежат множеству В и наоборот, все элементы множества В принадлежат множеству А.

Ни количество элементов, ни порядок их следования не имеет значения для равенства множества.

Пример: А={1; 2} и В={1, 2, 2, 1}, А=В.

2. Отношение включения

Говорят, что множество А включено (Ì ) в В, если все элементы множества А принадлежат В.

В этом случае множество А будем называть подмножеством В.

Если А={1, 2}, В={1, 2, 3}, то АÌВ.

Если А - студенты дошфака, В - студенты университета, то АÌВ.

3. Отношение пересечения

Говорят, что множества А и В пересекаются, если имеют хотя бы один общий элемент.

Например, А={1, 2, 3} и В={2, 4, 6} , А и В - пересекаются.

АВ

4. Если АÇВ=Æ, то множества А и В не пересекаются. Например, студенты 1 и 5 курсов – не пересекающиеся множества.