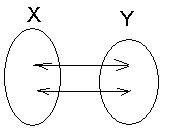
1 МНОЖЕСТВО. ЧИСЛО. СЧЕТ

Литература: [9, 11, 12, 14, 15, 16, 21, 22, 25, 31, 32, 34, 36]

Будько Т.С. Экскурсы ў матыматыку //Пралеска, № 8, 1994.

Глейзер Г.И. История математики в школе. IV-VI классы.

Энциклопедия для детей. Т. 11. Математика. – М., 1998.

История математики. Т. 1 /Под ред. Юшкевича А.Г. – М., 1970.

Фомин С.В. Системы счисления. – М., 1964.

1.1 Из истории развития количественных представлений

1.1.1 Этапы исторического развития числа

1 этап. Сравнение групп предметов по количеству с помощью установления взаимнооднозначного соответствия между элементами множеств (1 шкура - 1 горшок).

2 этап. Использование множеств-посредников для сравнения по количеству (зарубки на палке о количестве в прошлом году).

3 этап. Использование универсальных множеств для обозначения кол-ва (1 луна; 5 пальцев на руке: луна оленей; рука оленей).

4 этап. Возникновение числительных и нумерации, абстрагирование числа от конкретного множества.

5 этап. Становление теорий числа: количественной и порядковой.

1.1.2 Основные идеи количественной и порядковой теорий натурального числа

Количественная теория.

Г. Кантор, XIX в. Основные понятия – множество, взаимнооднозначное соответствие.

В том случае, если каждому элементу множества Х соответствует единственный элемент из множества У, то говорят, что между этими множествами установлено взаимнооднозначное соответствие.

Рассмотрим 2 бесконечных множества:

(1) множество натуральных чисел 1, 2, 3, 4, 5,…n, …

(2) множество четных натур. чисел 2, 4, 6,…2n, …( подмножество (1)).

Так как ряд четных чисел можно пронумеровать с помощью натуральных чисел, то между этими двумя множествами можно установить взаимнооднозначное соответствие. Если между множеством и его некоторым подмножеством нельзя установить взаимнооднозначное соответствие, то множество является конечным.