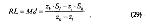Определение медианы, представленной в z-координатах психометрической функции, возможно графическим и расчетным путем. За абсолютный порог (и PSE при измерении двухкатегориальным методом констант разностного порога) принимается величина стимула, которой соответствует Z = 0. Стандартное отклонение определяется как такая величина стимула, для которой Z = +1 или Z = -1 (СНОСКА: Фактически шкала z-оценок и является шкалой единиц стандартного нормального отклонения — σ. Точка z=0 соответствует нулевому отклонению от среднего (медианы), точки z = l или -1 — отклонению от среднего на 1σ вправо или влево, соответственно). Через стандартное отклонение можно найти и величину полумежквартильного размаха — Q, т.к. их связь в случае нормального распределения описывается равенством

Для иллюстрации этого способа обработки обратимся к нашему примеру (см. табл. 2). Графическое представление зависимости величины Z"два" от физического параметра стимула (т.е. психометрическая функция в нормальных координатах) приведено на рис. 11.

Определение с помощью графиков параметров психометрической функции способом нормальной интерполяции не требует преобразования в z-координаты, если имеется в наличии вероятностная бумага. Способ изготовления такой бумаги подробно описан (Бардин, 1976).

Все необходимые пороговые показатели могут быть определены и аналитическим путем с помощью соответствующих формул. Для этого можно воспользоваться двумя методами.

Во-первых, можно применить уже известный нам метод линейной интерполяции (теперь в нормальных координатах), который фактически является аналогом простого графического решения, когда мы не производим строгого построения аппроксимирующей прямой. Расчет параметров психометрической прямой производится по формулам (29), (30) и (31):

где zl и zh— самые близкие к нулю отрицательная и положительная величины z, соответственно; Sl и Sh — стимулы, соответствующие zl и zh (т.е. величины ближайшего подпорогового и надпорогового стимулов).