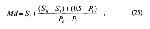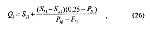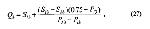Те же значения могут быть получены и расчетным путем по следующим формулам (фактически эти формулы вытекают из решения прямоугольных треугольников):

Медиана психометрической кривой определяется как

где Sl — величина ближайшего к 50-процентной точке стимула, лежащего ниже ее, Sh — величина стимула, лежащего непосредственно выше 50-процентной точки, Рl и Рh — соответствующие указанным выше стимулам пропорции ответов.

Первый и третий квартили вычисляются по формулам:

где Sl1 — величина стимула, лежащего непосредственно ниже 25-процентной точки,

Sh1 — величина стимула, лежащего непосредственно выше 25-процентной точки,

Р l1 и Рh1 — соответствующие указанным выше стимулам пропорции ответов.

где S l3 — величина стимула, лежащего непосредственно ниже 25-процентной точки; Sh3 — величина стимула, лежащего непосредственно выше 25-процентной точки; Рl3 и Рh3 — соответствующие указанным выше стимулам пропорции ответов.

В нашем примере Md = 10,57 мм, Q1 = 9,83 мм, Q3 = 11,33 мм.

Недостатками способа линейной интерполяции являются:

1) расточительность, так как из всех полученных в эксперименте данных используется только часть — например, для определения Md достаточно иметь две точки;

2) отсутствие возможности получить точную оценку показателей разброса — дисперсии или межквартильного размаха — Q. Если в эксперименте используется больше двух стимулов, можно определить Q1 и Q3, а если допустить, что распределение частот ответов является нормальным, то можно найти и величину стандартного отклонения через соотношение σ = 1,483Q. Однако при широком диапазоне используемых стимулов и относительно малом их числе (около 5, как в нашем примере) оценка Q будет не очень точной, следовательно, и значение σ также.

Способ нормальной интерполяции. Если сделать более строгое допущение о форме психометрической функции, а именно, что она является функцией нормального распределения, и если выразить масштаб оси ординат в единицах стандартного отклонения этого распределения, то психометрическая функция, имеющая S-образную форму в линейных координатах, превращается в прямую линию. После этого появляется возможность найти все интересующие исследователя параметры прямой, аналогично тому, как это делалось в случае линейной интерполяции. Но для этого нужно прежде всего преобразовать пропорции ответов Р с помощью таблиц нормального распределения в значения Z, представляющие собой нормированные по стандартному отклонению расстояния от стимульных точек до медианы. После преобразования Р в Z экспериментальные точки на графике, где по абсциссе отложен физический параметр стимула S, а по ординате — Z, могут быть аппроксимированы (СНОСКА: Термин "аппроксимация" экспериментальных точек какой-либо функцией означает процедуру представления (моделирования) набора эмпирических точек в виде определенной математической функции. В данном случае предполагается, что, если психометрическая функция — это функция нормального распределения, то в нормальных координатах она будет иметь вид линейной функции. Очевидно, что "хорошеть" арппок-симации экспериментальных точек линейной функцией будет одновременно служить показателем адекватности принятого предположения о нормальности распределения) прямой линией, которая проводится "на глазок" (этот способ хотя и прост, но чаще всего дает лишь грубое приближение), либо рассчитывается с помощью метода наименьших квадратов. Этот метод позволяет получить не только наилучшую аппроксимацию, но и статистически строго оценить степень "хорошести" подгонки полученной прямой к экспериментальным точкам.