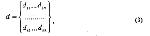Формально общая задача МШ выражается следующим образом. По заданной симметричной матрице различий между стимулами

нужно построить метрическую и пространственную модели стимулов, т.е. определить размерность пространства и координаты точек-стимулов в этом пространстве

таким образом, чтобы матрица расстояний, вычисленных между точками на основании метрической модели расстояния

была бы в смысле некоторого критерия возможно более близка к исходной матрице различий D (Терехина, 1986).

В МШ существуют два подхода к решению общей задачи — метрический и неметрический. В метрическом МШ на первом этапе строится модель субъективного расстояния. Исходные оценки сходств или различий преобразуются таким образом, чтобы числовые значения удовлетворяли аксиомам геометрического расстояния. На втором этапе по матрице абсолютных расстояний рассчитываются координаты точек и определяется размерность пространства. Для неметрического шкалирования существенными являются не абсолютные числовые значения оценок сходства, а только их порядок. Пространственная модель строится прямо по исходным данным о сходствах или различиях, при этом предполагается, что исходные оценки и межточечные расстояния связаны некоторой неизвестной и монотонной зависимостью, т.е. порядок межточечных расстояний должен соответствовать порядку исходных оценок.

Очевидно, что если исходные данные представлены в виде действительной симметричной матрицы порядка n с элементами не равными нулю, то всегда можно получить конфигурацию точек в пространстве размерности (n-1), удовлетворяющую этому условию. Однако если учитывать главную задачу МШ — определение минимальной размерности пространства, то задача построения пространственной модели сразу становится нетривиальной. Это наглядно иллюстрируется теоремой Гуттмана, которая гласит, что элементы действительной симметричной матрицы порядка n могут быть строго монотонны с расстояниями между п точками в действительном евклидовом пространстве размерностью не более, чем (n-2), только в том случае, если элементы матрицы не равны нулю и не совпадают друг с другом.